Kolorowe czapeczki – kontynuacja
Niedługo po ukazaniu się mojego artykułu Kolorowe czapeczki do redakcji przyszedł list od wieloletniego Czytelnika Delty, Jana Błaszczyńskiego, z propozycją rozwiązania postawionego tam problemu. Proste rozwiązanie Jana Błaszczyńskiego, w przeciwieństwie do przedstawionego w moim artykule, jest deterministyczne 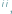 i na dodatek pozwala rozstrzygnąć problem dla dowolnej liczby kolorów czapeczek i dowolnej liczby krasnoludków.
i na dodatek pozwala rozstrzygnąć problem dla dowolnej liczby kolorów czapeczek i dowolnej liczby krasnoludków.
Dwa dni później przyszedł list od innego Czytelnika artykułu, studenta pierwszego roku matematyki stosowanej na Politechnice Gdańskiej, Marcina Krzywkowskiego, proponujący inne rozwiązanie, też proste i deterministyczne. Propozycja Marcina Krzywkowskiego omija dodatkowe założenie zawarte w rozwiązaniu Jana Błaszczyńskiego, ale ogranicza się do dwóch rodzajów czapeczek.
Oryginalne zadanie było takie:
Zadanie. Królewna Śnieżka wezwała siedmiu krasnoludków i oświadczyła, że w związku z wielkim świętem w najbliższą niedzielę postanowiła nagrodzić ich pracowitość.
- Przygotowałam dla was białe i kolorowe czapeczki. Nie powiem wam, ani ile białych, ani ile kolorowych czapeczek przygotowałam. Każdemu z was nałożę jedną z czapeczek na głowę, ale by było bardziej uroczyście, przedtem zgaszę światło. Po zapaleniu światła zobaczycie czapeczki u swoich kolegów, ale swojej nie będziecie mogli zobaczyć. Każdy z was dostanie 2 kartki ze swoim imieniem i napisem: Mam białą czapeczkę albo Mam kolorową czapeczkę. Jeśli któryś z was zechce, powinien wybrać jedną z nich i wrzucić do koszyka na środku sali. Ale pamiętajcie! Nie wolno wam się porozumiewać! Wspaniała nagroda - tu Królewna uśmiechnęła się tajemniczo - będzie wam wręczona, jeśli okaże się, że nikt się nie pomylił, a przynajmniej jedna osoba zgadła, jaką ma czapeczkę na głowie.
Rozwiązania Czytelników Delty
Warunki zadania pozwalają ustalić wcześniej strategię postępowania. W obu rozwiązaniach krasnoludki umawiają się działać "na tempo". W rozwiązaniu Jana Błaszczyńskiego tempo wyznacza kolejność, w jakiej krasnoludki będą wrzucać kartki do koszyka. Marcin Krzywkowski proponuje, aby krasnoludki podejmowały działanie co ustalony odcinek czasu, na przykład co 5 sekund.
Jan Błaszczyński zaproponował rozwiązanie przy dodatkowym założeniu, że na głowach krasnoludków są wszystkie rodzaje czapeczek. Warunkiem koniecznym do rozwiązania jest ubranie krasnoludków we wszystkie rodzaje czapeczek - skoro Śnieżka przygotowała białe i czerwone czapeczki, to z każdego rodzaju istnieje co najmniej jedna - pisze autor. Warunek ten przenosi on na przypadek dowolnej liczby rodzajów czapeczek - ma być reprezentowany każdy spośród 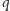 typów czapeczek.
typów czapeczek.
Rozwiązanie to najprościej przedstawić w postaci grafu.
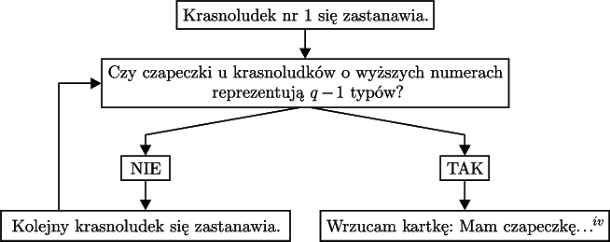
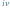 Tu krasnoludek wpisuje typ, którego brakuje.
Tu krasnoludek wpisuje typ, którego brakuje.
Gdy krasnoludek nr 1 widzi czapeczki 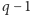 typów, wie, że jego czapeczka ma typ, którego brakuje i daje odpowiedź poprawną. Gdy krasnoludek nr 1 nie wrzuca kartki, to oznacza, że nie widzi
typów, wie, że jego czapeczka ma typ, którego brakuje i daje odpowiedź poprawną. Gdy krasnoludek nr 1 nie wrzuca kartki, to oznacza, że nie widzi 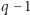 typów czapeczek. Gdyby tych typów było mniej niż
typów czapeczek. Gdyby tych typów było mniej niż  to wraz z jego czapeczką mogłoby być mniej niż
to wraz z jego czapeczką mogłoby być mniej niż 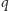 typów, co jest sprzeczne z założeniem, że wszystkie typy czapeczek są reprezentowane. Tak więc na głowach krasnoludków innych niż nr 1 są reprezentowane wszystkie typy. Sytuacja początkowa się powtarza, ale z mniejszą o 1 liczbą krasnoludków. W
typów, co jest sprzeczne z założeniem, że wszystkie typy czapeczek są reprezentowane. Tak więc na głowach krasnoludków innych niż nr 1 są reprezentowane wszystkie typy. Sytuacja początkowa się powtarza, ale z mniejszą o 1 liczbą krasnoludków. W 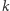 -tym kroku albo krasnoludek zobaczy
-tym kroku albo krasnoludek zobaczy 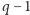 typów czapeczek, albo wśród
typów czapeczek, albo wśród 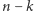 pozostałych krasnoludków są reprezentowane wszystkie typy czapeczek. Najpóźniej
pozostałych krasnoludków są reprezentowane wszystkie typy czapeczek. Najpóźniej 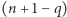 -ty krasnoludek zobaczy u swoich kolegów o wyższych numerach
-ty krasnoludek zobaczy u swoich kolegów o wyższych numerach 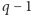 różnych typów, co kończy zgadywanie.
różnych typów, co kończy zgadywanie.
Podobne w pomyśle rozwiązanie dla dwóch kolorów czapeczek i dowolnej liczby 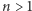 krasnoludków proponuje Marcin Krzywkowski.
krasnoludków proponuje Marcin Krzywkowski.
Krok 0 (5 sekund od początku)
Do koszyka podchodzą wyłącznie ci, którzy widzą czapeczki jednego koloru. Są możliwe 3 przypadki:
- Podszedł jeden krasnoludek - wtedy wrzuca kartkę z kolorem innym niż widzi.
- Podszedł więcej niż jeden krasnoludek - wtedy każdy z nich wrzuca kartkę z kolorem takim, jak widzi.
- Nie podszedł żaden krasnoludek - wtedy każdy krasnoludek widzi co najmniej jedną czapeczkę każdego koloru.
Krok 1 (10 sekund od początku)
Do koszyka podchodzą wyłącznie ci, którzy widzą dokładnie jedną czapeczkę koloru A i więcej niż jedną czapeczkę koloru B. Każdy z nich wnioskuje, że ma na głowie czapeczkę koloru A i taką kartkę wrzuca do koszyka.
Jeżeli do koszyka nie podszedł żaden krasnoludek, to każdy z nich widzi co najmniej po dwie czapeczki każdego koloru.
Krok 2 (15 sekund od początku)
Do koszyka podchodzą wyłącznie ci, którzy widzą dokładnie dwie czapeczki koloru A i więcej niż dwie czapeczki koloru B. Każdy z nich wnioskuje, że ma na głowie czapeczkę koloru A i taką kartkę wrzuca do koszyka.
Jeżeli do koszyka nie podszedł żaden krasnoludek, to każdy z nich widzi co najmniej po trzy czapeczki każdego koloru. Wykonujemy krok 3.
Ogólnie, jeżeli w 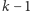 kroku do koszyka nie podszedł żaden krasnoludek, to każdy z nich widzi co najmniej po
kroku do koszyka nie podszedł żaden krasnoludek, to każdy z nich widzi co najmniej po 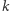 czapeczek każdego koloru. I wtedy wykonuje się następujący krok.
czapeczek każdego koloru. I wtedy wykonuje się następujący krok.
Krok 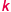 (
( 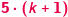 sekund od początku)
sekund od początku)
Do koszyka podchodzą wyłącznie ci, którzy widzą dokładnie 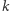 czapeczek koloru A i więcej niż
czapeczek koloru A i więcej niż 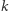 czapeczek koloru B. Każdy z nich wnioskuje, że ma na głowie czapeczkę koloru A i taką kartkę wrzuca do koszyka.
czapeczek koloru B. Każdy z nich wnioskuje, że ma na głowie czapeczkę koloru A i taką kartkę wrzuca do koszyka.
Postępowanie to musi się skończyć sukcesem wcześniej niż w kroku o numerze 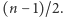
Dlaczego oryginalne rozwiązanie jest tak skomplikowane?
Oba rozwiązania przysłane przez Czytelników łamią założenie o tym, że podczas zgadywania nie wolno się porozumiewać. Przedstawione rozwiązania pozwalają kolejnym krasnoludkom przekazać swoją wiedzę poprzez fakt wstrzymania się od wrzucania kartek i wykonywanie tych gestów w kolejnych "krokach". Takie działanie jest z założenia niedozwolone.
To jednak ja nieświadomie sprowokowałem możliwość innej interpretacji założeń. W pierwotnej wersji artykułu każdy krasnoludek miał do wyboru trzy kartki: Mam białą czapeczkę, Mam kolorową czapeczkę i Rezygnuję z odpowiedzi. Ponadto na dany sygnał każdy z krasnoludków w tym samym czasie musiałby wrzucić do koszyka jedną z trzech kartek.
Złośliwy chochlik namówił mnie, żeby skrócić opis i zamiast polecenia wrzucenia kartki Rezygnuję z odpowiedzi zaproponowałem rezygnację z wrzucania. Przy okazji wypadł z tekstu artykułu nakaz jednoczesnego wrzucenia kartek.
Dzięki temu poznaliśmy jednak dwa ciekawe rozwiązania nieco innego zadania.
Propozycja
Nie jest znane rozwiązanie dla 3 typów czapeczek i  krasnoludków. Rozwiązanie Wesołka z artykułu
krasnoludków. Rozwiązanie Wesołka z artykułu  daje prawdopodobieństwo sukcesu
daje prawdopodobieństwo sukcesu 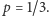 Oczekujemy propozycji rozwiązań o jak największym prawdopodobieństwie sukcesu dla 3 typów czapeczek i
Oczekujemy propozycji rozwiązań o jak największym prawdopodobieństwie sukcesu dla 3 typów czapeczek i  krasnoludków. Na początek dla
krasnoludków. Na początek dla 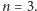 Najciekawsze rozwiązania przedstawimy w Delcie.
Najciekawsze rozwiązania przedstawimy w Delcie.
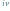 Tu krasnoludek wpisuje typ, którego brakuje.
Tu krasnoludek wpisuje typ, którego brakuje.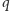 kroków przed końcem zgadywania.
kroków przed końcem zgadywania.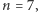 ale łatwo zobaczyć, że podane rozwiązanie jest poprawne dla dowolnego
ale łatwo zobaczyć, że podane rozwiązanie jest poprawne dla dowolnego 
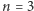 ), to jego kolega z czapeczką A na głowie musiałby widzieć, że pierwszy krasnoludek ma na głowie czapeczkę A, więc trzeci krasnoludek z czapeczką B widzi tylko jeden kolor A. A to stanowi sprzeczność z faktem, że każdy widzi co najmniej dwa kolory.
), to jego kolega z czapeczką A na głowie musiałby widzieć, że pierwszy krasnoludek ma na głowie czapeczkę A, więc trzeci krasnoludek z czapeczką B widzi tylko jeden kolor A. A to stanowi sprzeczność z faktem, że każdy widzi co najmniej dwa kolory.