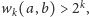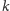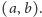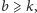Wielkie granie
O grze w 20 pytań inaczej
W artykule „Gra w 20 pytań” omówiliśmy sposób gry z graczem, który nie kłamie. A jak postępować z graczem, który kłamie? Czy jesteśmy zupełnie bezradni?
To pytanie postawił Stanisław Ulam w swojej książce Adventures of a
Mathematician. Zapytał on mianowicie o to, jaka jest najmniejsza możliwa
liczba pytań, które musi zadać Pytający, by odgadnąć pomyślaną liczbę z
przedziału
 jeżeli wiadomo, że Odpowiadający może raz
skłamać? Strategia wygrywająca oczywiścieistnieje: powtarzamy każde
pytanie 3 razy.
jeżeli wiadomo, że Odpowiadający może raz
skłamać? Strategia wygrywająca oczywiścieistnieje: powtarzamy każde
pytanie 3 razy.
Zajmiemy się od razu problemem ogólnym: Odpowiadający wybiera liczbę z
przedziału domkniętego
 Pytający zadaje
Pytający zadaje
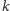 pytań,
Odpowiadającemu wolno raz skłamać. Podobnie, jak poprzednio, Pytający
zadaje pytania typu „czy
pytań,
Odpowiadającemu wolno raz skłamać. Podobnie, jak poprzednio, Pytający
zadaje pytania typu „czy
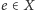 ?”, gdzie
?”, gdzie
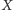 jest dowolnym
podzbiorem przedziału
jest dowolnym
podzbiorem przedziału
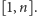 W tej postaci problem został niedawno
rozwiązany przez Andrzeja Pelca z Kanady. Problem analogiczny, w którym
zadawane pytania muszą być porównawcze, nie jest jeszcze rozwiązany do
końca. Przedstawimy teraz rozwiązanie oryginalnego problemu Ulama, dowód
będzie niewielką modyfikacją dowodu Pelca.
W tej postaci problem został niedawno
rozwiązany przez Andrzeja Pelca z Kanady. Problem analogiczny, w którym
zadawane pytania muszą być porównawcze, nie jest jeszcze rozwiązany do
końca. Przedstawimy teraz rozwiązanie oryginalnego problemu Ulama, dowód
będzie niewielką modyfikacją dowodu Pelca.
Zauważmy najpierw, że w każdym momencie naszej gry musimy
rozpatrywać dwa zbiory dopuszczalnych liczb (a nie jeden zbiór, jak w
przypadku gry bez kłamstw). Pierwszy z tych zbiorów składa się z tych liczb,
które są zgodne ze wszystkimi dotychczas udzielonymi odpowiedziami – tzn.
liczb o tej własności, że gdyby Odpowiadający pomyślał którąś z
nich, to w dotychczasowych odpowiedziach jeszcze nie skłamał, ma więc
prawo skłamać w dalszym ciągu gry. Drugi z tych zbiorów składa się z
liczb, spełniających wszystkie odpowiedzi z wyjątkiem jednej – są to więc
liczby, o których Odpowiadający już skłamał. Niech pierwszy zbiór ma
 elementów, a drugi
elementów, a drugi
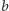 elementów. Parę
elementów. Parę
 nazwiemy stanem gry. Teraz zauważmy, że każde pytanie jest w istocie
rzeczy pytaniem o pewną liczbę elementów każdego z rozważanych
powyżej zbiorów. Przypuśćmy zatem, że pytamy o
nazwiemy stanem gry. Teraz zauważmy, że każde pytanie jest w istocie
rzeczy pytaniem o pewną liczbę elementów każdego z rozważanych
powyżej zbiorów. Przypuśćmy zatem, że pytamy o
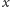 elementów
pierwszego zbioru i
elementów
pierwszego zbioru i
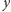 elementów drugiego. W zależności od
odpowiedzi, gra przejdzie ze stanu
elementów drugiego. W zależności od
odpowiedzi, gra przejdzie ze stanu
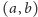 w jeden z dwóch stanów
oznaczanych dalej przez TAK i NIE. Zastanówmy się, jaką postać ma
stan TAK. Niech
w jeden z dwóch stanów
oznaczanych dalej przez TAK i NIE. Zastanówmy się, jaką postać ma
stan TAK. Niech
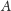 będzie pierwszym zbiorem (ma on
będzie pierwszym zbiorem (ma on
 elementów) i
elementów) i
 drugim zbiorem (o
drugim zbiorem (o
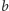 elementach). Pytanie „czy
elementach). Pytanie „czy
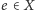 ?” jest pytaniem o
?” jest pytaniem o
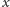 elementów zbioru
elementów zbioru
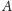 i
i
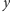 elementów zbioru
elementów zbioru
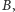 tzn. zbiór
tzn. zbiór
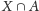 ma
ma
 elementów i
zbiór
elementów i
zbiór
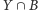 ma
ma
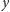 elementów. Zatem zbiory
elementów. Zatem zbiory
 i
i
 mają odpowiednio po
mają odpowiednio po
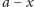 i
i
 elementów. W
przypadku odpowiedzi „tak” pierwszy zbiór będzie się składał z tych
elementów zbioru
elementów. W
przypadku odpowiedzi „tak” pierwszy zbiór będzie się składał z tych
elementów zbioru
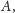 które są zgodne z ostatnią odpowiedzią,
czyli należą do
które są zgodne z ostatnią odpowiedzią,
czyli należą do
 Jest to zatem zbiór
Jest to zatem zbiór
 Do drugiego
zbioru należą natomiast te elementy zbioru
Do drugiego
zbioru należą natomiast te elementy zbioru
 o których teraz
skłamaliśmy (tzn.
o których teraz
skłamaliśmy (tzn.
 ) oraz te elementy zbioru
) oraz te elementy zbioru
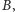 o
których nie skłamaliśmy (tzn.
o
których nie skłamaliśmy (tzn.
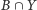 ). Stan TAK jest zatem równy
). Stan TAK jest zatem równy
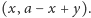 Podobnie rozumując stwierdzimy, że stan NIE ma postać
Podobnie rozumując stwierdzimy, że stan NIE ma postać
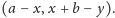
Z każdym stanem zwiążemy teraz funkcję zwaną jego wagą. Przypuśćmy,
że w stanie
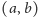 Pytający może zadać jeszcze
Pytający może zadać jeszcze
 pytań. Wtedy
kładziemy
pytań. Wtedy
kładziemy
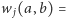
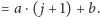 Funkcję
Funkcję
 nazwiemy
właśnie funkcją wagi (dokładniej
nazwiemy
właśnie funkcją wagi (dokładniej
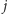 -tą wagą) stanu
-tą wagą) stanu
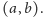 Funkcja
wagi mówi nam, jakie możliwości ma jeszcze Odpowiadający. Ma on do
dyspozycji
Funkcja
wagi mówi nam, jakie możliwości ma jeszcze Odpowiadający. Ma on do
dyspozycji
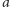 liczb, o których dotychczas mówił prawdę, może więc o
każdej z nich dalej mówić prawdę lub skłamać w jednym z następnych
liczb, o których dotychczas mówił prawdę, może więc o
każdej z nich dalej mówić prawdę lub skłamać w jednym z następnych
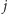 pytań – daje to
pytań – daje to
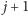 możliwości dla każdej z tych
możliwości dla każdej z tych
 liczb. Wreszcie ma on do dyspozycji
liczb. Wreszcie ma on do dyspozycji
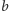 liczb, o których
musi mówić prawdę do końca. Następnie określmy tzw. charakter
stanu
liczb, o których
musi mówić prawdę do końca. Następnie określmy tzw. charakter
stanu

Zauważmy na koniec, że

W dalszym ciągu będziemy wielokrotnie zastanawiali się nad istnieniem strategii
wygrywającej dla Pytającego w środkowej fazie gry. Jeżeli gra znalazła się w
stanie
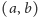 i Pytający ma od tego momentu strategię wygrywającą za
pomocą co najwyżej
i Pytający ma od tego momentu strategię wygrywającą za
pomocą co najwyżej
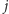 pytań, to będziemy nazywać ją strategią
wygrywającą począwszy od tego stanu.
pytań, to będziemy nazywać ją strategią
wygrywającą począwszy od tego stanu.
Dowód. Odpowiadający może zastosować diabelską strategię (patrz Mała Delta). Po pierwszym pytaniu będziemy mieli nierówność

Stąd jeden ze stanów TAK i NIE ma
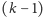 -szą wagę większą
od
-szą wagę większą
od
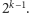 Odpowiadający wybiera tę odpowiedź, która ma większą
wagę. W ten sposób po
Odpowiadający wybiera tę odpowiedź, która ma większą
wagę. W ten sposób po
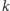 pytaniach dojdzie do stanu, którego
zerowa waga jest co najmniej równa 2. Teraz wystarczy zauważyć, że
Pytający ma pewność zgadnięcia po zadaniu wszystkich pytań tylko
wtedy, gdy stan gry jest jednym ze stanów (1,0) lub (0,1). Oba te stany
mają jednak zerową wagę równą 1. Diabelska strategia okazała się zatem
skuteczna dla Odpowiadającego, co kończy dowód lematu.
pytaniach dojdzie do stanu, którego
zerowa waga jest co najmniej równa 2. Teraz wystarczy zauważyć, że
Pytający ma pewność zgadnięcia po zadaniu wszystkich pytań tylko
wtedy, gdy stan gry jest jednym ze stanów (1,0) lub (0,1). Oba te stany
mają jednak zerową wagę równą 1. Diabelska strategia okazała się zatem
skuteczna dla Odpowiadającego, co kończy dowód lematu.
Z powyższego lematu wynika, że Pytający może mieć strategię wygrywającą
w
 pytaniach tylko wtedy, gdy
pytaniach tylko wtedy, gdy
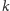 -ta waga stanu początkowego jest
co najwyżej równa
-ta waga stanu początkowego jest
co najwyżej równa
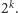 W szczególności może się zdarzyć, że
Pytający ma strategię wygrywającą w
W szczególności może się zdarzyć, że
Pytający ma strategię wygrywającą w
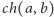 pytaniach począwszy od
stanu
pytaniach począwszy od
stanu
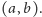 Pokażemy teraz, że tak jest w istocie dla bardzo obszernej
klasy stanów.
Pokażemy teraz, że tak jest w istocie dla bardzo obszernej
klasy stanów.
Nazwijmy stan
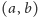 stanem przyjemnym, jeśli Pytający ma strategię
wygrywającą w
stanem przyjemnym, jeśli Pytający ma strategię
wygrywającą w
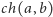 pytaniach począwszy od stanu
pytaniach począwszy od stanu
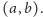 Stan
Stan
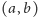 nazwiemy stanem typowym, jeśli
nazwiemy stanem typowym, jeśli

Twierdzenie. Wszystkie stany typowe są przyjemne.
Dowód. Jedynymi stanami o charakterze 0 są stany (1,0) i (0,1). Są one stanami przyjemnymi, bo Pytający zna pomyślaną liczbę bez zadawania jakichkolwiek pytań.
Przypuśćmy teraz, że wszystkie stany typowe o charakterze
mniejszym od
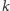 są przyjemne. Niech
są przyjemne. Niech
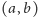 będzie dowolnym
stanem typowym charakteru
będzie dowolnym
stanem typowym charakteru
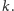 Pokażemy, że jest on przyjemny.
W tym celu wystarczy znaleźć takie pytanie, że otrzymane w jego
wyniku stany mają
Pokażemy, że jest on przyjemny.
W tym celu wystarczy znaleźć takie pytanie, że otrzymane w jego
wyniku stany mają
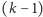 -sze wagi różniące się co najwyżej
o 1. Mianowicie z założenia o charakterze stanu
-sze wagi różniące się co najwyżej
o 1. Mianowicie z założenia o charakterze stanu
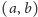 wiemy,
że
wiemy,
że
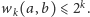 Jeśli teraz
Jeśli teraz
 to
to
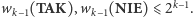 Stąd wynika, że charakter stanów
TAK i NIE jest co najwyżej równy
Stąd wynika, że charakter stanów
TAK i NIE jest co najwyżej równy
 Jeśli teraz uda nam się
dobrać pytanie tak, aby stany TAK i NIE były typowe, to z założenia
będą one przyjemne. Pytający ma zatem strategię wygrywającą w
Jeśli teraz uda nam się
dobrać pytanie tak, aby stany TAK i NIE były typowe, to z założenia
będą one przyjemne. Pytający ma zatem strategię wygrywającą w
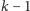 pytaniach, co łącznie z zadanym już pierwszym pytaniem daje strategię
wygrywającą w
pytaniach, co łącznie z zadanym już pierwszym pytaniem daje strategię
wygrywającą w
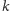 pytaniach.
pytaniach.
Przypadek 1. Niech
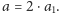 W zależności od parzystości liczby
W zależności od parzystości liczby
 bierzemy liczbę
bierzemy liczbę
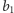 tak,
by
tak,
by
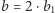 lub
lub
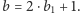 Wystarczy zadać teraz pytanie
o
Wystarczy zadać teraz pytanie
o
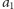 elementów pierwszego zbioru i
elementów pierwszego zbioru i
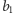 elementów drugiego
zbioru. Otrzymamy stany typowe
elementów drugiego
zbioru. Otrzymamy stany typowe

których wagi różnią się, oczywiście, co najwyżej o 1.
Przypadek 2. Niech
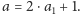 Udowodnimy najpierw pomocniczy lemat.
Udowodnimy najpierw pomocniczy lemat.
Dowód. Bierzemy takie liczby
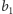 i
i
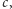 by
by
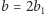 lub
lub
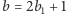 oraz
oraz
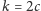 lub
lub
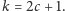 Zadajemy teraz
pytanie o
Zadajemy teraz
pytanie o
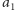 elementów pierwszego zbioru i
elementów pierwszego zbioru i
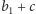 elementów
drugiego zbioru. Otrzymamy stany typowe
elementów
drugiego zbioru. Otrzymamy stany typowe

różniące się wagami co najwyżej o 1:

Niech teraz
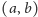 będzie stanem typowym, takim, że
będzie stanem typowym, takim, że
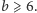 Pokażemy, że wtedy
Pokażemy, że wtedy
 czyli spełnione jest założenie lematu 2.
Otóż wystarczy pokazać, że
czyli spełnione jest założenie lematu 2.
Otóż wystarczy pokazać, że
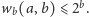

Ostatnią nierówność sprawdza się łatwo przez indukcję względem
 co skończy dowód lematu.
co skończy dowód lematu.
Niech teraz
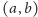 będzie stanem typowym, takim, że
będzie stanem typowym, takim, że
 Wtedy
Wtedy
 i z powyższych rozważań wynika, że istnieje
poszukiwane pytanie. Pozostają do rozpatrzenia przypadki stanów
i z powyższych rozważań wynika, że istnieje
poszukiwane pytanie. Pozostają do rozpatrzenia przypadki stanów
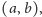 takich, że
takich, że

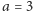 lub
lub
 oraz
oraz
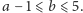 Znalezienie w każdym z tych przypadków (z wyjątkiem stanu (3,2)) pytania,
takiego, że stany TAK i NIE mają wagi różniące się co najwyżej o 1, jest
łatwym ćwiczeniem dla Czytelnika. W stanie (3,2), który ma charakter 5,
zadajemy pytanie o 2 elementy pierwszego zbioru, otrzymując w wyniku stany
(2,1) i (1,4). Teraz wystarczy zauważyć, że
Znalezienie w każdym z tych przypadków (z wyjątkiem stanu (3,2)) pytania,
takiego, że stany TAK i NIE mają wagi różniące się co najwyżej o 1, jest
łatwym ćwiczeniem dla Czytelnika. W stanie (3,2), który ma charakter 5,
zadajemy pytanie o 2 elementy pierwszego zbioru, otrzymując w wyniku stany
(2,1) i (1,4). Teraz wystarczy zauważyć, że
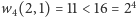 oraz
oraz
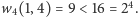 To kończy dowód twierdzenia.
To kończy dowód twierdzenia.
Udowodnione twierdzenie pozwala już na dokładne określenie liczby pytań
potrzebnych Pytającemu do odgadnięcia pomyślanej liczby. Ograniczymy się
w dalszym ciągu do szczególnego przypadku, gdy liczba
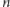 jest parzysta.
Rozważmy zatem stan
jest parzysta.
Rozważmy zatem stan
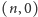 i przypuśćmy, że jego charakter
wynosi
i przypuśćmy, że jego charakter
wynosi
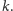 Zatem
Zatem
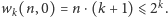 Zadamy pytanie o
Zadamy pytanie o
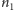 elementów (gdzie
elementów (gdzie
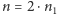 ). Otrzymamy w wyniku
tego pytania dwa identyczne stany
). Otrzymamy w wyniku
tego pytania dwa identyczne stany
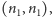 każdy o tej samej
wadze
każdy o tej samej
wadze
 Zatem
Zatem
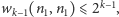 skąd wynika,
że otrzymane stany mają charakter równy co najwyżej
skąd wynika,
że otrzymane stany mają charakter równy co najwyżej
 Jednocześnie są one typowe, a więc z twierdzenia wynika, że są one
przyjemne. Oznacza to, że Pytający ma strategię wygrywającą w
Jednocześnie są one typowe, a więc z twierdzenia wynika, że są one
przyjemne. Oznacza to, że Pytający ma strategię wygrywającą w
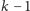 pytaniach, począwszy od każdego z tych stanów. Łącznie z pierwszym
pytaniem daje to strategię wygrywającą w
pytaniach, począwszy od każdego z tych stanów. Łącznie z pierwszym
pytaniem daje to strategię wygrywającą w
 pytaniach, począwszy od
stanu wyjściowego
pytaniach, począwszy od
stanu wyjściowego
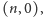 a więc od przedziału domkniętego
a więc od przedziału domkniętego
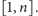
Z drugiej strony, jeśli
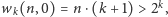 to Odpowiadający
ma swoją strategię diabelską. Ostatecznie dostajemy odpowiedź na pytanie,
kiedy Pytający ma strategię wygrywającą: strategia ta istnieje dla przedziału
domkniętego
to Odpowiadający
ma swoją strategię diabelską. Ostatecznie dostajemy odpowiedź na pytanie,
kiedy Pytający ma strategię wygrywającą: strategia ta istnieje dla przedziału
domkniętego
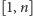 (dla
(dla
 parzystego) i
parzystego) i
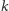 pytań wtedy i tylko
wtedy, gdy
pytań wtedy i tylko
wtedy, gdy
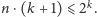 Analogiczne rozwiązanie dla
Analogiczne rozwiązanie dla
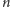 nieparzystego Czytelnik bez trudu znajdzie samodzielnie – jedyna drobna
trudność polega na tym, że po pierwszym pytaniu nie otrzymujemy
stanów identycznych. Najrówniejszy podział stanu
nieparzystego Czytelnik bez trudu znajdzie samodzielnie – jedyna drobna
trudność polega na tym, że po pierwszym pytaniu nie otrzymujemy
stanów identycznych. Najrówniejszy podział stanu
 dla
dla
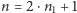 otrzymamy pytając o
otrzymamy pytając o
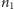 elementów – wynikiem będą
stany
elementów – wynikiem będą
stany
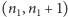 oraz
oraz
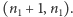 Z otrzymanej zależności po
chwili wynika, że dla
Z otrzymanej zależności po
chwili wynika, że dla
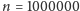 potrzeba 25 pytań. Jako ciekawostkę
można podać, że analogiczna gra z dwoma kłamstwami wymaga 29
pytań.
potrzeba 25 pytań. Jako ciekawostkę
można podać, że analogiczna gra z dwoma kłamstwami wymaga 29
pytań.
Analiza przedstawionego dowodu pozwala zauważyć, że pytania, które
będziemy zadawać, są pytaniami o przedział: „czy pomyślana liczba leży w
przedziale domkniętym
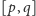 ?”.
?”.
Czytelnikom umiejącym pisać programy komputerowe można teraz zaproponować napisanie programu odgadującego pomyślaną liczbę według opisanego wyżej algorytmu.
Zastosowanie dla tego typu zabaw jest chyba widoczne. Chodzi mianowicie o
przesyłanie informacji kanałami, które czasami powodują powstawanie błędów.
Wystąpienie dwóch błędów jest bardzo mało prawdopodobne, spróbujmy więc
opracować metodę postępowania w przypadku pojawienia się co najwyżej
jednego błędu. Zobaczyliśmy pewną metodę postępowania w takich
przypadkach, mianowicie wtedy, gdy mamy do czynienia z interakcyjną wymianą
informacji. Można teraz wyobrazić sobie, że chcemy odgadnąć pomyślaną
liczbę, ale musimy zadać wszystkie pytania od razu. Pytania te będą,
oczywiście, znane Odpowiadającemu przed grą. Wystarczy więc, jeśli przyśle
on nam ciąg odpowiedzi, zakodowany w postaci ciągu zer i jedynek: zero na
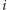 -tej pozycji oznacza, że na to pytanie dał odpowiedź negatywną,
jedynka – pozytywną. Problemem będzie teraz znalezienie minimalnej
długości kodu (i oczywiście sposobu rozkodowywania, czyli treści
kolejnych pytań), tak aby móc przesłać jednoznaczną informację o
pomyślanej liczbie, pomimo że zakodowany ciąg po odebraniu go może
różnić się na jednym miejscu od ciągu wysłanego. W ten sposób
doszliśmy do pojęcia tzw. kodów korygujących błędy, o których innym
razem.
-tej pozycji oznacza, że na to pytanie dał odpowiedź negatywną,
jedynka – pozytywną. Problemem będzie teraz znalezienie minimalnej
długości kodu (i oczywiście sposobu rozkodowywania, czyli treści
kolejnych pytań), tak aby móc przesłać jednoznaczną informację o
pomyślanej liczbie, pomimo że zakodowany ciąg po odebraniu go może
różnić się na jednym miejscu od ciągu wysłanego. W ten sposób
doszliśmy do pojęcia tzw. kodów korygujących błędy, o których innym
razem.