Jak zaparkować samochód?
Rozważmy następujący
Problem. Na pewnym parkingu znajduje się
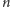 miejsc, ustawionych
w rzędzie, ponumerowanych liczbami naturalnymi
miejsc, ustawionych
w rzędzie, ponumerowanych liczbami naturalnymi
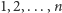 . Każdy
z parkujących tam
. Każdy
z parkujących tam
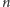 kierowców ma swoje ulubione miejsce: dla
kierowców ma swoje ulubione miejsce: dla
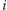 -tego kierowcy niech będzie to miejsce o numerze
-tego kierowcy niech będzie to miejsce o numerze
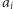 , przy czym
dla różnych kierowców miejsca te nie muszą być różne. Kierowcy
przyjeżdżają kolejno na parking: kiedy
, przy czym
dla różnych kierowców miejsca te nie muszą być różne. Kierowcy
przyjeżdżają kolejno na parking: kiedy
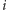 -ty kierowca wjeżdża na
parking, jedzie aż do swojego ulubionego miejsca, a następnie, jeśli jest
wolne, parkuje tam, jeśli zaś jest zajęte, parkuje na następnym wolnym
miejscu. Jeśli wszystkie następne miejsca są zajęte, odjeżdża. Spróbujemy
określić liczbę wszystkich takich ciągów preferencji
-ty kierowca wjeżdża na
parking, jedzie aż do swojego ulubionego miejsca, a następnie, jeśli jest
wolne, parkuje tam, jeśli zaś jest zajęte, parkuje na następnym wolnym
miejscu. Jeśli wszystkie następne miejsca są zajęte, odjeżdża. Spróbujemy
określić liczbę wszystkich takich ciągów preferencji
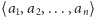 ,
że wszystkim kierowcom uda się zaparkować swoje samochody.
,
że wszystkim kierowcom uda się zaparkować swoje samochody.
Ciąg
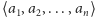 o wyrazach w zbiorze
o wyrazach w zbiorze
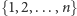 będziemy nazywać funkcją parkingową długości
będziemy nazywać funkcją parkingową długości
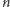 , jeśli wszystkim
kierowcom uda się zaparkować samochody.
, jeśli wszystkim
kierowcom uda się zaparkować samochody.
Na początek zobaczmy, ile wynosi liczba funkcji parkingowych długości
 dla
dla
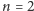 i
i
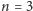 . Mamy mianowicie:
. Mamy mianowicie:
- (1)
- dla
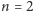 trzy takie ciągi: 11, 12, 21,
trzy takie ciągi: 11, 12, 21,
- (2)
- dla
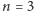 szesnaście takich ciągów: 111, 112, 121, 211, 113, 131,
311, 122, 212, 221, 123, 132, 213, 231, 312, 321.
szesnaście takich ciągów: 111, 112, 121, 211, 113, 131,
311, 122, 212, 221, 123, 132, 213, 231, 312, 321.
Problem wyznaczenia wszystkich funkcji parkingowych długości
 został
rozwiązany przez Pyke’a w 1959 roku oraz niezależnie przez Konheima
i Weissa w 1966 roku. Okazuje się mianowicie, że zachodzi następujące
został
rozwiązany przez Pyke’a w 1959 roku oraz niezależnie przez Konheima
i Weissa w 1966 roku. Okazuje się mianowicie, że zachodzi następujące
Twierdzenie. Liczba wszystkich funkcji parkingowych długości
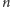 wynosi
wynosi
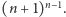
Dowód. Zmodyfikujmy nieco nasz problem: na początku parkingu (tj.
przed miejscem o numerze
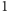 ) dodajemy miejsce
o numerze
) dodajemy miejsce
o numerze
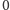 . Ponadto pozwalamy kierowcom, którym nie udało
się zaparkować zgodnie ze starymi regułami, przejechać przez parking
po raz drugi, począwszy od miejsca
. Ponadto pozwalamy kierowcom, którym nie udało
się zaparkować zgodnie ze starymi regułami, przejechać przez parking
po raz drugi, począwszy od miejsca
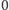 , aż do pierwszego wolnego
miejsca.
, aż do pierwszego wolnego
miejsca.
Oczywiście, teraz wszystkim kierowcom uda się zaparkować
samochody, a jedno miejsce pozostanie wolne. Łatwo zauważyć, że ciąg
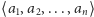 jest funkcją parkingową wtedy i tylko wtedy, gdy po
zaparkowaniu samochodów przez wszystkich kierowców miejsce
jest funkcją parkingową wtedy i tylko wtedy, gdy po
zaparkowaniu samochodów przez wszystkich kierowców miejsce
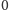 pozostanie wolne.
pozostanie wolne.
Niech
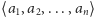 będzie dowolnym ciągiem o wyrazach
w zbiorze
będzie dowolnym ciągiem o wyrazach
w zbiorze
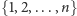 . Jeśli zgodnie z tym ciągiem
. Jeśli zgodnie z tym ciągiem
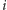 -ty
kierowca zaparkuje na miejscu
-ty
kierowca zaparkuje na miejscu
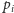 , to (dla
, to (dla
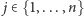 )
zgodnie z ciągiem
)
zgodnie z ciągiem

(oczywiście modulo
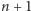 ) zaparkuje na miejscu
) zaparkuje na miejscu
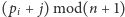 .
.
Dla każdego ciągu
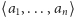 o wyrazach ze zbioru od 1
do
o wyrazach ze zbioru od 1
do
 rozważmy zbiór:
rozważmy zbiór:

Każdy taki ciąg wyznacza
 -elementowy podzbiór zbioru
-elementowy podzbiór zbioru
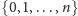 – zbiór tych miejsc, na których zaparkują kierowcy.
Odwrotnie: każdy taki podzbiór jest wyznaczony przez pewien ciąg
postaci
– zbiór tych miejsc, na których zaparkują kierowcy.
Odwrotnie: każdy taki podzbiór jest wyznaczony przez pewien ciąg
postaci
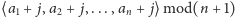 . Oczywiście,
tylko jeden
. Oczywiście,
tylko jeden
 -elementowy podzbiór zbioru
-elementowy podzbiór zbioru
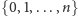 nie zawiera liczby
nie zawiera liczby
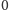 , a zatem tylko jeden ciąg z powyższego zbioru
jest funkcją parkingową.
, a zatem tylko jeden ciąg z powyższego zbioru
jest funkcją parkingową.
Suma wszystkich zbiorów
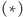 jest zbiorem wszystkich ciągów długości
jest zbiorem wszystkich ciągów długości
 o wyrazach
ze zbioru
o wyrazach
ze zbioru
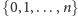 . Liczba takich ciągów wynosi
. Liczba takich ciągów wynosi
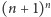 .
Zatem liczba funkcji parkingowych długości
.
Zatem liczba funkcji parkingowych długości
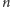 musi być równa
musi być równa

Funkcje parkingowe, o których mowa w powyższym twierdzeniu, znalazły
szereg zastosowań w kombinatoryce, a w szczególności w teorii grafów.
Jako przykład można przytoczyć twierdzenie Sylvestera, Borchardta
i Cayleya mówiące o tym, że liczba wszystkich lasów ukorzenionych
o
 ponumerowanych wierzchołkach jest równa liczbie funkcji
parkingowych długości
ponumerowanych wierzchołkach jest równa liczbie funkcji
parkingowych długości
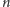 .
.
Czytelnik może w charakterze prostego ćwiczenia spróbować wykazać, że liczba niemalejących funkcji parkingowych wynosi dokładnie

Na koniec powiedzmy, że liczby tej postaci, zwane liczbami Catalana,
występują w wielu miejscach w bardzo różnych dziedzinach matematyki.
Kombinatorycznie liczby Catalana można zdefiniować na ponad
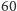 różnych sposobów. Dla przykładu, liczby Catalana to: liczba poprawnych
nawiasowań przy użyciu
różnych sposobów. Dla przykładu, liczby Catalana to: liczba poprawnych
nawiasowań przy użyciu
 par nawiasów, liczba ciągów
zero-jedynkowych zdominowanych przez
par nawiasów, liczba ciągów
zero-jedynkowych zdominowanych przez
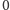 , liczba triangulacji
, liczba triangulacji
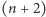 -kąta wypukłego. Ale to już zupełnie inna opowieść.
-kąta wypukłego. Ale to już zupełnie inna opowieść.