Mała Delta

Szuflady pana Dirichleta

Jeśli macie w biurku trzy szuflady, a chcecie do nich włożyć zeszyty z, powiedzmy, sześciu przedmiotów, to nie ma rady: w co najmniej jednej szufladzie muszą znaleźć się zeszyty z co najmniej dwóch przedmiotów.

Tę prostą obserwację można rozwinąć do następującej zasady ogólnej: jeśli rozmieścić 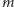$\text{[math]}$ przedmiotów w $\text{[math]}$ szufladach i $\text{[math]}$ , to w co najmniej jednej szufladzie znajdą się co najmniej dwa przedmioty. Ta ogólna zasada znana jest pod nazwą zasady szufladkowej Dirichleta. 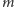Jej matematyczne sformułowanie brzmi tak: jeśli $\text{[math]}$ , to nie istnieje funkcja różnowartościowa ze zbioru $\text{[math]}$ -elementowego w zbiór $\text{[math]}$ -elementowy.

Oczywiście, szuflady mogą być przeróżne, w zależności od kontekstu, mogą nawet wcale nie przypominać fragmentu mebla. Istotne jest jedynie, co jesteśmy skłonni uznać za szufladę. Popatrzmy na dwa zadania, które można rozwiązać za pomocą zasady Dirichleta, odpowiednio interpretując pojęcia „szuflady” i „przedmiotu”.

Na początek zadanie geometryczne.

Spróbujmy teraz użyć zasady szufladkowej Dirichleta w następującym zadaniu.

Nie chcąc odbierać Czytelnikowi przyjemności wynikającej z samodzielnego rozwiązania zadania, proponuję następujące.

Powodzenia!