Odpowiedź (na obydwa pytania): 
Oznaczmy przez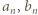 
odpowiedzi na pytania zadane, odpowiednio, w punktach (a) i (b). Bezpośrednio sprawdzamy, że 
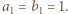Przyjmijmy dalej, że 
W części (a) zauważmy, że w pierwszym przejeździe z prawdopodobieństwem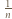 
Piotrek od razu zjedzie na parter oraz dla 
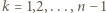z prawdopodobieństwem 
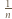znajdzie się na piętrze 
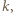a zatem w sytuacji, w której średni numer ostatniego piętra, które odwiedzi przed parterem, jest równy 
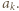Wobec tego
Podobnie w części (b) z prawdopodobieństwem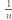 
Piotrek zjedzie na parter od razu oraz dla 
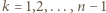z prawdopodobieństwem 
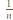znajdzie się w sytuacji, w której oczekiwana liczba dalszych przejazdów jest równa 
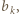czyli
Nietrudno zauważyć, że wyprowadzone rekurencyjne wzory na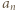 
oraz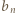 
są w istocie jednakowe, a zatem 
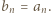Pozostaje rozwiązać tę rekurencję.
Korzystając z wyprowadzonej zależności dla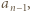 
uzyskujemy
skąd po podstawieniu do rekurencji dla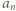 
mamy
Stąd wobec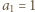 
wynika, że
Uwaga. Czytelnik Oblatany zauważy z pewnością, że wynik, czyli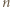 
-ta suma częściowa szeregu harmonicznego, jest oczekiwaną liczbą cykli w rozkładzie losowej permutacji zbioru 
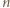-elementowego. Jeśli ponadto ów Czytelnik należy do zbioru Czytelników Ambitnych, polecamy Mu znalezienie kombinatorycznego uzasadnienia tego związku.