Umieśćmy schodkowy trójkąt w układzie współrzędnych w taki sposób, aby środki jego pól były w punktach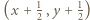 
dla wszystkich par liczb całkowitych nieujemnych 
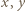takich, że 
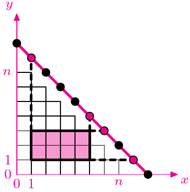
Zauważmy, że przedłużenia boków dowolnego prostokąta złożonego z całych pól schodkowego trójkąta przecinają prostą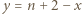 
w czterech różnych punktach spośród 
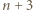następujących:
Odwrotnie, każde cztery różne punkty spośród powyższych wyznaczają dokładnie jeden prostokąt - dwa niższe punkty są zawarte w przedłużeniach poziomych boków prostokąta, a dwa wyższe - w przedłużeniach boków pionowych.
Zbudowana wzajemnie jednoznaczna odpowiedniość między szukanymi prostokątami a czwórkami spośród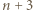 
ustalonych punktów świadczy o tym, że odpowiedź na postawione w zadaniu pytanie to