Deltoid
Trójkątne dowody
Symbol Newtona 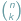 dla liczb całkowitych
dla liczb całkowitych 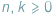 oznacza liczbę sposobów wybrania zbioru
oznacza liczbę sposobów wybrania zbioru 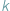 elementów spośród
elementów spośród 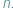 W szczególności
W szczególności 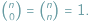
Ze zbioru 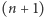 -elementowego z jednym elementem wyróżnionym
-elementowego z jednym elementem wyróżnionym 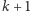 elementów można wybrać, biorąc wyróżniony element i
elementów można wybrać, biorąc wyróżniony element i 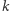 z pozostałych
z pozostałych 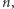 albo wybierając wszystkie
albo wybierając wszystkie 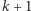 spośród
spośród 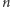 niewyróżnionych. Stąd
niewyróżnionych. Stąd 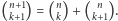
Z symboli Newtona można zbudować trójkąt Pascala (Rys. 1), w którym w 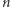 -tym wierszu (numerując od 0) stoją kolejno wartości
-tym wierszu (numerując od 0) stoją kolejno wartości 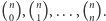
Na mocy powyższych wzorów liczby wzdłuż ramion trójkąta są równe 1, a wewnątrz każda liczba jest sumą dwóch liczb stojących nad nią 
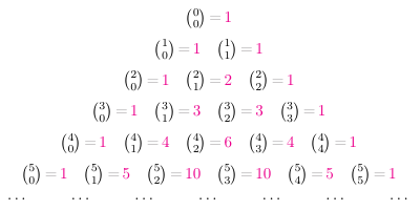
Rys. 1 Każda jedynka prócz 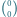 też spełnia warunek
też spełnia warunek 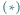 : jest sumą jedynki nad nią i umownego zera na zewnątrz trójkąta.
: jest sumą jedynki nad nią i umownego zera na zewnątrz trójkąta.
Korzystając z trójkąta Pascala i własności 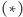 można udowodnić wiele tożsamości.
można udowodnić wiele tożsamości.
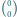 też spełnia warunek
też spełnia warunek 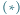 : jest sumą jedynki nad nią i umownego zera na zewnątrz trójkąta.
: jest sumą jedynki nad nią i umownego zera na zewnątrz trójkąta.