Kącik początkującego olimpijczyka
Nic nie może przecież wiecznie trwać
O półniezmiennikach, dzięki którym wykazujemy, że pewne przekształcenia można wykonać tylko skończenie wiele razy.
Zajmiemy się tu takimi półniezmiennikami, które robią coś zupełnie innego niż niezmienniki - są narzędziami w dowodzeniu, że z danego obiektu, przy użyciu wybranych przekształceń, jest możliwe - lub wręcz nieuniknione - osiągnięcie obiektu o pożądanej własności.
Następujący przykład powinien to rozjaśnić.
Przykład. Na płaszczyźnie narysowano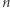 
odcinków, których końce są różne i żadne trzy końce nie leżą na jednej prostej. Ruch polega na wybraniu dwóch przecinających się odcinków - powiedzmy 
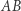i 
- i 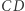zastąpieniu ich odcinkam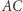i 
i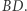 
Wykazać, że nieuniknione jest osiągnięcie stanu, w którym żadne dwa z tych odcinków się nie przecinają.
Z każdym ruchem maleje suma długości narysowanych odcinków (to jest poszukiwany półniezmiennik), która może przyjąć jedynie skończenie wiele różnych wartości. Z tego wynika, że w pewnym momencie nie będzie już można wykonać ruchu - a to świadczy o tym, że żadne odcinki się nie przecinają.
W zadaniach 1, 2, 5 i 6 stosujemy podobne rozumowanie, by wykazać nieuniknioność końca niezależnie od tego, które z dostępnych przekształceń w danym momencie wybrano. W pozostałych zadaniach musimy sterować przekształceniami w odpowiedni sposób.