Co żarówka ma do cewki?

Czasami pozornie proste sprzęty domowego użytku mogą dostarczyć ciekawych pytań dla fizyka. Na przykład: czy włókno żarówki zasilanej prądem zmiennym zmienia swoją temperaturę? Jeżeli tak, to ile wynosi amplituda tych zmian i jaką funkcją możemy opisać ich przebieg czasowy? Robi się jeszcze ciekawiej, gdy okazuje się, że problem ten można sprowadzić do zagadnienia analogicznego do przepływu prądu przez cewkę!

Będę rozważał żarówkę 100 W zasilaną prądem zmiennym o częstotliwości 50 Hz. Przyjmuję, że średnia temperatura włókna wynosi 3000 K. Można się spodziewać, że odchylenia od średniej temperatury będą niewielkie.

Żarówka wypromieniowuje ciepło zgodnie z prawem Stefana-Boltzmanna:

P(T ) =σ xST 4,

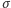gdzie $σ$ - stała Stefana-Boltzmanna, 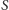$S$ - pole powierzchni włókna, 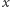$|x$ - współczynnik szarości włókna. Dla uproszczenia wprowadzę stałą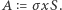 $|A$

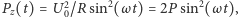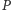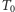Moc chwilowa źródła prądu jest dana wzorem: $Pz(t) = U2$ gdzie $| P$ jest średnią mocą żarówki. W opisie zakładamy, że opór żarówki jest stały, ponieważ spodziewamy się niewielkich odchyleń temperatury od średniej, a co za tym idzie - małych zmian oporu. Temperaturę wygodnie jest zapisać w postaci: $T = T0 +τ(t),$ gdzie $|T0$ jest średnią temperaturą. Zmiana temperatury jest opisywana równaniem:

C

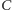gdzie $C$ jest pojemnością cieplną włókna żarówki. Ponieważ 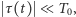$(t) τ ≪ T0,$ możemy użyć przybliżenia: 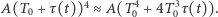$| A(T0$ Następnie korzystając z tożsamości 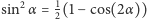$2 1 sin α = 2(1− cos(2α ))$ oraz równości 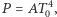$|P = AT$ otrzymujemy

C

Zapisując ostatnie równanie w innej formie:

P cos(2ω

zauważamy analogię z równaniem opisującym cewkę podłączoną do źródła napięcia zmiennego (patrz margines): $U0$ Korzystając z tego, można obliczyć amplitudę zmian temperatury i przesunięcie fazowe między napięciem a temperaturą:

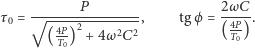τ0 = √-----P--------, tgϕ = 2ω---. ( 4P-)2 + 4ω ( 4PT0) T0

(1)

Korzystając z tej analogii, otrzymujemy zależność temperatury włókna od czasu:

T (t) = T0− τ0cos(2ω

gdzie amplituda 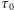$τ0$ i przesunięcie fazowe 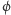$ϕ$ dane są wzorami (1).

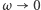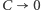Powyższe równanie pociąga za sobą zależności, których oczekiwalibyśmy intuicyjnie, tj. wzrost których wartości zwiększa amplitudę, a których zmniejsza. Wątpliwości mogą budzić przypadki $|ω$ i $|C$ (wtedy amplituda dąży do 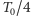$T0/4$ ). Należy przy tym jednak pamiętać, że traci wówczas sens założenie o małej wartości amplitudy i wynikające z niego przybliżenia.

Uwzględnijmy na końcu dane liczbowe - moc wynosi 100 W, częstotliwość 50 Hz, średnia temperatura to 3000 K, wartość masy $m$ przyjmuję jako 28 mg (zgodnie z pomiarami przeprowadzonymi przez Szymona Weltera i Alexandra Stefaniego, którzy wyznaczyli ją dzięki uprzejmości Instytutu Fizyki UMK). Dla takich danych otrzymujemy amplitudę temperatury równą 42 K, co zgadza się z przyjętym założeniem, że amplituda jest znacznie mniejsza od średniej temperatury włókna.

Autor chciałby wyrazić podziękowania dla doktora Macieja Wiśniewskiego za wsparcie i cenne rady podczas pisania artykułu.