Klub 44F - zadania IV 2014»Zadanie 577
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IV 2014
- Publikacja w Delcie: kwiecień 2014
- Publikacja elektroniczna: 31 marca 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (232 KB)
Na powierzchni długiego, nieprzewodzącego walca o promieniu
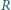 równomiernie rozłożony jest ładunek o gęstości powierzchniowej
równomiernie rozłożony jest ładunek o gęstości powierzchniowej
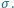 Walec znajduje się w jednorodnym polu magnetycznym o indukcji
Walec znajduje się w jednorodnym polu magnetycznym o indukcji
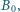 którego linie są równoległe do osi walca. Znaleźć prędkość
kątową walca po wyłączeniu zewnętrznego pola magnetycznego. Walec ma
jednorodną gęstość
którego linie są równoległe do osi walca. Znaleźć prędkość
kątową walca po wyłączeniu zewnętrznego pola magnetycznego. Walec ma
jednorodną gęstość
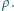

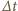 czas, w którym następuje wyłączenie zewnętrznego
pola magnetycznego. Zmiana strumienia tego pola przez powierzchnię przekroju
poprzecznego walca powoduje powstanie stycznego do powierzchni walca pola
elektrycznego, które działa na ładunek na powierzchni walca i wywołuje jego
obrót. Z kolei poruszający się ładunek powierzchniowy wytwarza wewnątrz
walca dodatkowe pole magnetyczne, które zgodnie z regułą przekory
rośnie w czasie i skierowane jest zgodnie z polem
czas, w którym następuje wyłączenie zewnętrznego
pola magnetycznego. Zmiana strumienia tego pola przez powierzchnię przekroju
poprzecznego walca powoduje powstanie stycznego do powierzchni walca pola
elektrycznego, które działa na ładunek na powierzchni walca i wywołuje jego
obrót. Z kolei poruszający się ładunek powierzchniowy wytwarza wewnątrz
walca dodatkowe pole magnetyczne, które zgodnie z regułą przekory
rośnie w czasie i skierowane jest zgodnie z polem
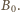 Oznaczmy
maksymalną wartość wektora tego pola przez
Oznaczmy
maksymalną wartość wektora tego pola przez
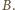 Zgodnie z prawem
Faradaya
Zgodnie z prawem
Faradaya
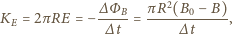
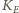 oznaczyliśmy krążenie pola elektrycznego
oznaczyliśmy krążenie pola elektrycznego
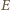 wzdłuż
okręgu o promieniu
wzdłuż
okręgu o promieniu
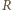 otaczającego przekrój poprzeczny walca, a przez
otaczającego przekrój poprzeczny walca, a przez
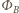 strumień pola magnetycznego przez powierzchnię tego przekroju.
Wartość indukowanego pola magnetycznego, gdy obracający się walec osiągnie
końcową prędkość kątową
strumień pola magnetycznego przez powierzchnię tego przekroju.
Wartość indukowanego pola magnetycznego, gdy obracający się walec osiągnie
końcową prędkość kątową
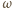 wynosi
wynosi
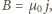 gdzie
gdzie
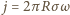 jest natężeniem prądu na jednostkę długości walca. Średni
moment siły zwiększający prędkość kątową walca w czasie
jest natężeniem prądu na jednostkę długości walca. Średni
moment siły zwiększający prędkość kątową walca w czasie
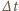 dany jest
wzorem
dany jest
wzorem
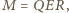 gdzie
gdzie
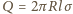 jest całkowitym ładunkiem
na powierzchni walca o długości
jest całkowitym ładunkiem
na powierzchni walca o długości
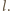 Równanie ruchu obrotowego walca
ma postać
Równanie ruchu obrotowego walca
ma postać
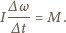
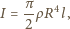
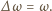 Wstawiając natężenie pola
Wstawiając natężenie pola
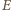 z prawa Faradaya
do równania ruchu obrotowego, otrzymujemy szukaną prędkość
kątową:
z prawa Faradaya
do równania ruchu obrotowego, otrzymujemy szukaną prędkość
kątową:
