Klub 44F - zadania IV 2017»Zadanie 636
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IV 2017
- Publikacja w Delcie: kwiecień 2017
- Publikacja elektroniczna: 30 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (75 KB)
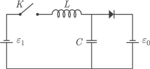
Rys. 1
W obwodzie przedstawionym na rysunku 1 mamy 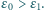 Jaki ładunek przepłynie przez źródło o sile elektromotorycznej
Jaki ładunek przepłynie przez źródło o sile elektromotorycznej 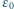 po zamknięciu klucza
po zamknięciu klucza 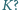 Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.
Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.


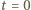 natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
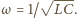 W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła
W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła 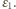 Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu
Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu 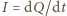 spada do zera, ładunek na kondensatorze osiąga maksymalną wartość
spada do zera, ładunek na kondensatorze osiąga maksymalną wartość 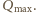 Zgodnie z zasadą zachowania energii mamy
Zgodnie z zasadą zachowania energii mamy 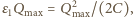 czyli maksymalne napięcie na kondensatorze wynosi
czyli maksymalne napięcie na kondensatorze wynosi 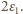
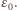 Gdy
Gdy 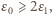 przez źródło o sile elektromotorycznej
przez źródło o sile elektromotorycznej 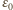 nie przepłynie żaden ładunek.
nie przepłynie żaden ładunek.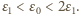 Gdy napięcie na kondensatorze osiąga wartość
Gdy napięcie na kondensatorze osiąga wartość 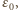 prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem
prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem 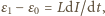 czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez
czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez 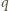 szukany ładunek przepływający przez źródło o sile elektromotorycznej
szukany ładunek przepływający przez źródło o sile elektromotorycznej 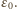 Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło
Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło 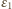 przepływa ładunek
przepływa ładunek 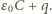 Bilans energetyczny dla całego procesu ma postać
Bilans energetyczny dla całego procesu ma postać 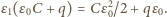 Stąd
Stąd