Klub 44F - zadania II 2018»Zadanie 652
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania II 2018
- Publikacja w Delcie: luty 2018
- Publikacja elektroniczna: 1 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (112 KB)
Znaleźć przyspieszenie, z jakim spada pionowo w dół okrągła metalowa płytka o masie  w jednorodnym polu magnetycznym o indukcji
w jednorodnym polu magnetycznym o indukcji 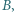 równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki
równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki 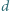 jest dużo mniejsza od jej promienia
jest dużo mniejsza od jej promienia 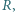 przyspieszenie ziemskie ma wartość
przyspieszenie ziemskie ma wartość 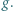

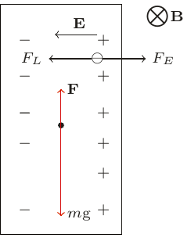
 Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza
Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza 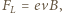 gdzie
gdzie  jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego
jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego 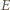 skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną
skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną 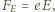 czyli zachodzi związek
czyli zachodzi związek 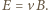 Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi
Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi 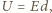 a ładunek na powierzchniach
a ładunek na powierzchniach 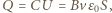 gdzie
gdzie 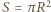 jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu
jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu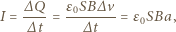
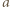 jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość
jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość 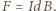 Równanie ruchu płytki ma postać
Równanie ruchu płytki ma postać 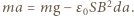 Stąd szukane przyspieszenie jest równe
Stąd szukane przyspieszenie jest równe