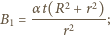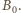Klub 44F - zadania IV 2016»Zadanie 617
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IV 2016
- Publikacja w Delcie: kwiecień 2016
- Publikacja elektroniczna: 30 marca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)

Na zewnątrz powierzchni walcowej o promieniu  wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie:
wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie: 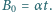 Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu
Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu 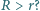 W chwili
W chwili 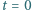 elektron spoczywa.
elektron spoczywa.

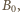 ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu
ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu 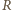 i ma w danej chwili prędkość
i ma w danej chwili prędkość 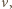 to działająca na niego siła dośrodkowa jest siłą Lorentza:
to działająca na niego siła dośrodkowa jest siłą Lorentza: 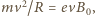 zatem jego prędkość
zatem jego prędkość 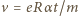 rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej
rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej 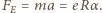 Wektor natężenia pola elektrycznego o długości
Wektor natężenia pola elektrycznego o długości 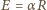 jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu
jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu 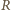 ma wartość bezwzględną
ma wartość bezwzględną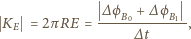
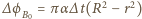 jest zmianą w czasie
jest zmianą w czasie 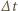 strumienia pola
strumienia pola 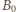 przez powierzchnię objętą okręgiem,
przez powierzchnię objętą okręgiem, 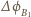 jest zmianą strumienia szukanego pola
jest zmianą strumienia szukanego pola 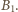 Ponieważ
Ponieważ 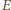 nie zależy od czasu,
nie zależy od czasu, 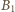 musi być liniową funkcją czasu:
musi być liniową funkcją czasu: