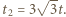Klub 44F - zadania I 2018»Zadanie 651
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2018
- Publikacja w Delcie: styczeń 2018
- Publikacja elektroniczna: 1 stycznia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (86 KB)
Dwie jednakowo naładowane kulki o takich samych masach umieszczono w odległości 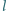 od siebie i puszczono swobodnie. Po czasie
od siebie i puszczono swobodnie. Po czasie 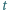 odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić
odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić 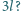

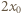 i obliczmy ich prędkości
i obliczmy ich prędkości 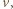 gdy odległość ta osiągnie wartość
gdy odległość ta osiągnie wartość 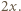 Z zasady zachowania energii otrzymujemy
Z zasady zachowania energii otrzymujemy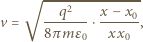
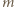 jest masą, a
jest masą, a 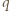 ładunkiem kulki.
ładunkiem kulki.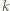 oraz położenia początkowego
oraz położenia początkowego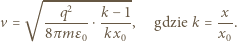
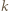 zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których
zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których 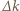 są takie same. Przemieszczenie kulki przy zmianie
są takie same. Przemieszczenie kulki przy zmianie 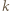 o
o 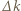 wynosi
wynosi 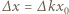 i w drugim przypadku jest 3 razy większe niż w pierwszym:
i w drugim przypadku jest 3 razy większe niż w pierwszym: 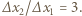 Z
Z 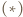 wynika, że dla danego
wynika, że dla danego 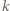 prędkość kulki w pierwszym przypadku jest
prędkość kulki w pierwszym przypadku jest 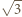 razy większa niż w drugim. Przy zmianie
razy większa niż w drugim. Przy zmianie 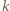 o małe
o małe 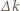 średnie prędkości kulek również będą różnić się
średnie prędkości kulek również będą różnić się 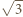 razy:
razy: 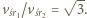 Czasy, w których kulki przemieszczają się o
Czasy, w których kulki przemieszczają się o 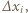 są równe:
są równe: 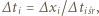 gdzie
gdzie 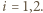 Stosunek tych czasów w rozważanych przypadkach dany jest wzorem
Stosunek tych czasów w rozważanych przypadkach dany jest wzorem 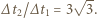 Całkowity czas ruchu w drugim przypadku wynosi
Całkowity czas ruchu w drugim przypadku wynosi