Klub 44F - zadania IX 2018»Zadanie 663
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IX 2018
- Publikacja w Delcie: wrzesień 2018
- Publikacja elektroniczna: 27 sierpnia 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (69 KB)

W kondensatorze płaskim jedna okładka jest nieruchoma, a druga może poruszać się bez tarcia i jest połączona ze ścianą za pomocą sprężyny o współczynniku sprężystości 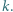 Pole powierzchni każdej okładki wynosi
Pole powierzchni każdej okładki wynosi 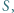 początkowa odległość między nimi
początkowa odległość między nimi 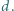 Okładki podłączono do źródła napięcia stałego. Przy jakiej maksymalnej wartości tego napięcia okładki nie zetkną się, jeżeli są stale równoległe względem siebie?
Okładki podłączono do źródła napięcia stałego. Przy jakiej maksymalnej wartości tego napięcia okładki nie zetkną się, jeżeli są stale równoległe względem siebie?

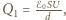 a jego energia wynosi
a jego energia wynosi 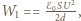 gdzie
gdzie 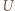 jest napięciem między okładkami a
jest napięciem między okładkami a 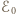 przenikalnością elektryczną próżni. Załóżmy, że ruchoma okładka zatrzyma się, gdy sprężyna zostanie rozciągnięta o
przenikalnością elektryczną próżni. Załóżmy, że ruchoma okładka zatrzyma się, gdy sprężyna zostanie rozciągnięta o 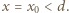 Do chwili zatrzymania ładunek na kondensatorze wzrośnie do wartości
Do chwili zatrzymania ładunek na kondensatorze wzrośnie do wartości 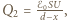 energia osiągnie wartość
energia osiągnie wartość 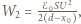 a źródło wykona pracę
a źródło wykona pracę 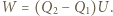 Zasada zachowania energii ma postać
Zasada zachowania energii ma postać 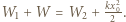 Otrzymujemy stąd równanie
Otrzymujemy stąd równanie 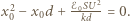 Ma ono rozwiązanie, gdy
Ma ono rozwiązanie, gdy 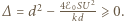 Stąd szukana maksymalna wartość napięcia
Stąd szukana maksymalna wartość napięcia 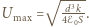 Odpowiadająca jej odległość między okładkami ma wartość
Odpowiadająca jej odległość między okładkami ma wartość 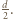
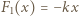 i siła przyciągania elektrostatycznego między okładkami
i siła przyciągania elektrostatycznego między okładkami 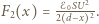 Jeżeli okładka zatrzyma się, gdy
Jeżeli okładka zatrzyma się, gdy 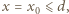 to jej zmiana energii kinetycznej wynosi
to jej zmiana energii kinetycznej wynosi 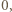 a z drugiej strony równa jest pracy wypadkowej siły działającej na okładkę:
a z drugiej strony równa jest pracy wypadkowej siły działającej na okładkę: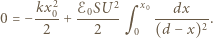
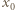 jak w poprzednim rozwiązaniu.
jak w poprzednim rozwiązaniu.