Klub 44F - zadania X 2012»Zadanie 544
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania X 2012
- Publikacja w Delcie: październik 2012
- Publikacja elektroniczna: 30 września 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (90 KB)
Cienkościenna, nieprzewodząca sfera o promieniu
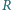 i masie
i masie
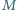 naładowana jest równomiernie ładunkiem
naładowana jest równomiernie ładunkiem
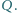 W sferze
znajdują się dwa niewielkie otwory leżące na tej samej średnicy. Cząstka
o masie
W sferze
znajdują się dwa niewielkie otwory leżące na tej samej średnicy. Cząstka
o masie
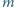 i ładunku
i ładunku
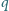 jednoimiennym z
jednoimiennym z
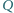 zaczyna
zbliżać się do sfery z bardzo dużej odległości wzdłuż prostej przechodzącej
przez otwory, z prędkością początkową
zaczyna
zbliżać się do sfery z bardzo dużej odległości wzdłuż prostej przechodzącej
przez otwory, z prędkością początkową
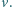 W chwili początkowej sfera
spoczywa. Ile czasu cząstka znajdować się będzie wewnątrz sfery? Przyjmij, że
efekty magnetyczne są zaniedbywalne.
W chwili początkowej sfera
spoczywa. Ile czasu cząstka znajdować się będzie wewnątrz sfery? Przyjmij, że
efekty magnetyczne są zaniedbywalne.

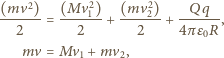
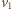 i
i
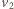 są odpowiednio prędkościami sfery i cząstki
w chwili, gdy cząstka dotrze do pierwszego otworu. Musi być spełniony
warunek
są odpowiednio prędkościami sfery i cząstki
w chwili, gdy cząstka dotrze do pierwszego otworu. Musi być spełniony
warunek
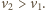 Wiemy z prawa Gaussa, że wewnątrz równomiernie
naładowanej sfery nie ma pola elektrycznego, cząstka porusza się więc od jednego
do drugiego otworu ruchem jednostajnym prostoliniowym z prędkością
względną
Wiemy z prawa Gaussa, że wewnątrz równomiernie
naładowanej sfery nie ma pola elektrycznego, cząstka porusza się więc od jednego
do drugiego otworu ruchem jednostajnym prostoliniowym z prędkością
względną
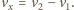 Szukany czas wynosi
Szukany czas wynosi
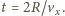
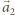 i
i
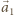 odpowiednio cząstki i sfery w dowolnym
układzie inercjalnym wynoszą
odpowiednio cząstki i sfery w dowolnym
układzie inercjalnym wynoszą
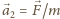 i
i
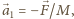 gdzie
gdzie
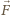 jest siłą, jaką sfera działa na cząstkę wzdłuż wektora położenia
względnego obu ciał, a jej wartość zależy od odległości między
nimi. Przyspieszenie względne wynosi
jest siłą, jaką sfera działa na cząstkę wzdłuż wektora położenia
względnego obu ciał, a jej wartość zależy od odległości między
nimi. Przyspieszenie względne wynosi
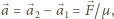 gdzie
gdzie
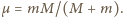 Jest to równanie ruchu fikcyjnej cząstki o masie
Jest to równanie ruchu fikcyjnej cząstki o masie
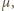 zwanej masą zredukowaną układu dwóch ciał, poruszającej się z ich
prędkością względną w polu siły
zwanej masą zredukowaną układu dwóch ciał, poruszającej się z ich
prędkością względną w polu siły
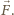 Zasada zachowania energii
w naszym problemie sprowadzonym do ruchu jednego ciała ma teraz
postać
Zasada zachowania energii
w naszym problemie sprowadzonym do ruchu jednego ciała ma teraz
postać
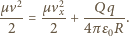
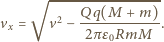
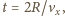 gdy
gdy
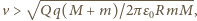 dla
mniejszych prędkości cząstka nie dotrze do wnętrza sfery.
dla
mniejszych prędkości cząstka nie dotrze do wnętrza sfery.