Zadanie ZF-907
o zadaniu...
- Publikacja w Delcie: lipiec 2016
- Publikacja elektroniczna: 1 lipca 2016
Skolimowana wiązka protonów ma kształt walca o promieniu 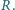 Protony wiązki poruszają się ze stałą prędkością
Protony wiązki poruszają się ze stałą prędkością 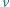 równolegle do osi wiązki. Jaka siła działa na proton poruszający się w odległości
równolegle do osi wiązki. Jaka siła działa na proton poruszający się w odległości 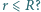 Przyjmujemy, że wewnątrz wiązki liczba protonów na jednostkę objętości jest stała i wynosi
Przyjmujemy, że wewnątrz wiązki liczba protonów na jednostkę objętości jest stała i wynosi 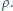

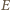 i
i 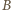 wzdłuż wiązki są równe zeru. Z symetrii układu wynika, że dla każdej wartości
wzdłuż wiązki są równe zeru. Z symetrii układu wynika, że dla każdej wartości  różne od zera mogą być tylko składowa pola
różne od zera mogą być tylko składowa pola 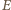 prostopadła do osi wiązki, skierowana od osi wiązki na zewnątrz i składowa pola
prostopadła do osi wiązki, skierowana od osi wiązki na zewnątrz i składowa pola 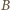 prostopadła do pola
prostopadła do pola 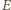 i do prędkości
i do prędkości 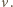 Wartości
Wartości 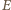 i
i 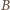 są przy tym jedynie funkcjami odległości
są przy tym jedynie funkcjami odległości  od osi wiązki. Na podstawie prawa Gaussa (obliczamy strumień
od osi wiązki. Na podstawie prawa Gaussa (obliczamy strumień 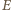 przez powierzchnię walca) mamy
przez powierzchnię walca) mamy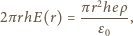
 oznacza ładunek protonu,
oznacza ładunek protonu, 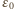 to przenikalność dielektryczna próżni, a
to przenikalność dielektryczna próżni, a 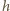 - "grubość plasterka" wiązki. Prawo Ampère'a (obliczamy krążenie wzdłuż okręgu o środku w centrum wiązki) prowadzi natomiast do równania
- "grubość plasterka" wiązki. Prawo Ampère'a (obliczamy krążenie wzdłuż okręgu o środku w centrum wiązki) prowadzi natomiast do równania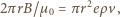
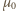 jest przenikalnością magnetyczną próżni. Podstawiając otrzymane w ten sposób wartości
jest przenikalnością magnetyczną próżni. Podstawiając otrzymane w ten sposób wartości 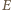 i
i 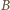 do wzoru na siłę Lorentza, otrzymujemy, że na proton wiązki działa siła
do wzoru na siłę Lorentza, otrzymujemy, że na proton wiązki działa siła 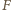 prostopadła do osi wiązki i skierowana na zewnątrz wiązki:
prostopadła do osi wiązki i skierowana na zewnątrz wiązki: