Eksperyment, który przeprowadzimy, będzie miał tym razem charakter ilościowego pomiaru fizycznego, a nie, jak w zeszłym miesiącu, jakościowej obserwacji zjawiska.

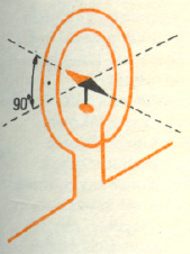
Na czym rzecz polega, czyli idea doświadczenia.

Wyznaczymy indukcję ziemskiego pola magnetycznego, a ściślej jej poziomą składową, przez pomiar częstości wahań igły magnetycznej. Niestety częstość ta zależy nie tylko od szukanej wartości indukcji, ale i od innych parametrów układu doświadczalnego, jak moment magnetyczny czy moment bezwładności igły. Dla ich odseparowania będziemy musieli nieco zmodyfikować pomiar.

Nieco teorii, albo dlaczego igła się waha?

Igle magnetycznej, podobnie jak każdemu namagnesowanemu przedmiotowi możemy przypisać moment magnetyczny 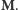W polu magnetycznym o indukcji 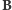na igłę działa więc moment siły Przechodząc do wartości liczbowych mamy:

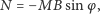gdzie 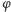jest kątem odchylenia. Minus przed prawą stroną oznacza, że moment siły działa w kierunku przeciwnym do wychylenia. Dla małych kątów 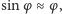a wtedy:

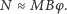(1)

Mamy więc moment siły proporcjonalny do wychylenia, własność, która charakteryzuje ruch harmoniczny. Jak wiemy przyśpieszenie w ruchu harmonicznym jest równe:

gdzie 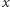jest wychyleniem, a 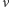częstością drgań. W ruchu obrotowym analogiczna zależność istnieje między przyśpieszeniem kątowym i kątem wychylenia :

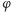Z II zasady dynamiki dla ruchu obrotowego mamy:

gdzie 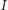jest momentem bezwładności. Wobec tego w ruchu harmonicznym:

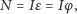Porównując ten wzór z (1) mamy:

(2)

Otrzymany wzór określa zależność między częstością wahań igły i szukaną indukcją 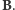Musimy jeszcze pozbyć się występujących tu nieznanych wielkośc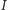i i 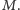W tym celu wytworzymy pewne znane dodatkowe pole magnetyczne 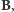(a jak - o tym za chwilę) i wykonamy dwa pomiary częstości wahań: 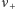- kiedy zwrot dodatkowego pola 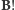będzie zgodny ze zwrotem pola ziemskiego 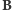oraz 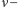- kiedy zwroty te będą przeciwne. Na podstawie (2) będziemy mieli:

oraz (dla ):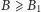

Przez podzielenie stronami otrzymujemy:

i po prostym przekształceniu:

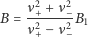(3)

Jak to zrobić czyli przebieg doświadczenia

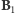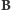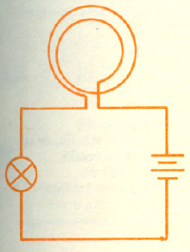
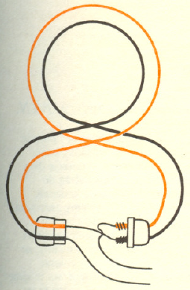
Dodatkowe pole wytworzymy przy pomocy przewodnika kołowego z prądem (o zwojach). Aby kierunki pól i 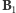były zgodne, należy ustawić przewodnik kołowy tak, aby jego płaszczyzna była prostopadła do kierunku swobodnej igły magnetycznej. Jako źródła prądu użyjemy bateryjki. W obwód włączymy, także żaróweczkę dla ustalenia wartości natężenia prądu. Schemat obwodu przedstawia rysunek. Praktycznie wygodnie posłużyć się latarką kieszonkową, w której obwód włączymy szeregowo przewodnik kołowy. W okrągłej latarce najlepiej zrobić to odkręcając jej tylną zakrętkę (ze sprężyną) i podłączając się między obudowę a dno baterii. Kto nie dysponuje przewodem izolowanym, może zrobić przewodnik kołowy nawijając długi przedłużacz lub sznur od żelazka na jakąś okrągłą formę np. kosz od śmieci. Połączenie należy tak wykonać, aby wykorzystać oba przewody przedłużacza łącząc je szeregowo. Oczywiście liczbę zwojów będziemy wtedy liczyć podwójnie. Indukcję 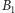(w 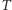) obliczymy ze wzoru:

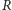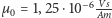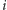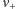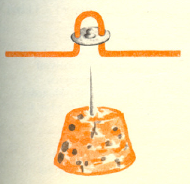
gdzie jest promieniem przewodnika kołowego, a przenikalnością magnetyczną próżni. Natężenie (jeśli nie dysponujemy amperomierzem) odczytamy po prostu z cokołu żaróweczki przy założeniu, że siła elektromotoryczna baterii zgadza się z napięciem nominalnym żaróweczki, wypisanym na niej, a opór przewodu i opór wewnętrzny baterii jest do pominięcia. Częstości i 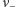mierzymy, licząc wahnięcia w ciągu np. 1 minuty. Kto nie ma igły magnetycznej czy kompasu, może ją zrobić z kawałka drutu i dużego zatrzasku, namagnesować magnesem i osadzić na igle do szycia wbitej tępym końcem w korek.

Napiszcie, jak Wam się udało.