Indukcja matematyczna... w układach oporników

Rys. 1 Ograniczamy się tylko do przypadku, gdy oporniki połączone są w sposób szeregowo-równoległy, tzn. nie ma żadnych gwiazdek, trójkątów itp.

Rys. 2
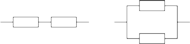
Rys. 3
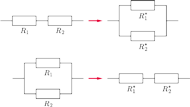
Rys. 4a – góra i Rys. 4b – dół.
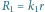 i
i
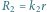 oznaczają opory zastępcze
podukładów, a
oznaczają opory zastępcze
podukładów, a
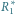 i
i
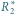 oznaczają opory zastępcze podukładów, w których
połączenia równoległe zastąpiono szeregowymi i odwrotnie.
oznaczają opory zastępcze podukładów, w których
połączenia równoległe zastąpiono szeregowymi i odwrotnie.
Rozważmy układ oporników o jednakowym oporze
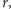 połączonych –
na przykład – tak, jak na rysunku 1. .
połączonych –
na przykład – tak, jak na rysunku 1. .
Zmieniamy wszystkie połączenia równoległe na szeregowe, a szeregowe – na równoległe (Rys. 2).
Jak łatwo obliczyć, opór zastępczy wyjściowego układu jest równy
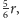 a zmienionego
a zmienionego
 Zauważmy, że iloczyn współczynników
bezwymiarowych jest równy 1, czyli jeden z nich jest odwrotnością
drugiego. Nie jest to przypadek. Wykażemy, że jeśli mamy układ
Zauważmy, że iloczyn współczynników
bezwymiarowych jest równy 1, czyli jeden z nich jest odwrotnością
drugiego. Nie jest to przypadek. Wykażemy, że jeśli mamy układ
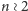 oporników o jednakowym oporze
oporników o jednakowym oporze
 i jego opór zastępczy
jest równy
i jego opór zastępczy
jest równy
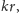 to – po zamianie wszystkich połączeń szeregowych
na równoległe i odwrotnie – opór zastępczy nowego układu oporników jest
równy
to – po zamianie wszystkich połączeń szeregowych
na równoległe i odwrotnie – opór zastępczy nowego układu oporników jest
równy
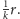
Zastosujemy zasadę indukcji matematycznej względem
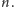 Dla
Dla
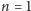 twierdzenie jest trywialne. Dla
twierdzenie jest trywialne. Dla
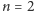 mamy dwie
możliwości (Rys. 3).
mamy dwie
możliwości (Rys. 3).
Nasze twierdzenie jest wówczas prawdziwe, gdyż opór zastępczy połączenia
szeregowego jest równy
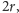 równoległego zaś
równoległego zaś
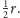
Niech
 będzie ustaloną liczbą naturalną. Załóżmy, że twierdzenie jest
prawdziwe dla wszystkich liczb naturalnych nie większych od
będzie ustaloną liczbą naturalną. Załóżmy, że twierdzenie jest
prawdziwe dla wszystkich liczb naturalnych nie większych od
 Wykażemy,
że jest ono prawdziwe dla układu
Wykażemy,
że jest ono prawdziwe dla układu
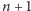 oporników. W tym celu
rozbijemy go na dwa podukłady. Połączenia „końcowe” tych podukładów
można przedstawić tak, jak na rysunkach 4a i 4b .
oporników. W tym celu
rozbijemy go na dwa podukłady. Połączenia „końcowe” tych podukładów
można przedstawić tak, jak na rysunkach 4a i 4b .
Z założenia indukcyjnego otrzymujemy

Opór zastępczy układu w przypadku a) jest równy
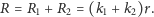 | (1) |
Obliczamy opór zastępczy
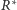 po zmianie. Mamy
po zmianie. Mamy
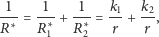 |
skąd
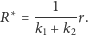 | (2) |
Wobec tego, na podstawie równości (1) i (2) mamy tezę indukcyjną.
Rozważania w przypadku b) są podobne.
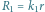 i
i
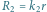 oznaczają opory zastępcze
podukładów, a
oznaczają opory zastępcze
podukładów, a
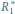 i
i
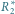 oznaczają opory zastępcze podukładów, w których
połączenia równoległe zastąpiono szeregowymi i odwrotnie.
oznaczają opory zastępcze podukładów, w których
połączenia równoległe zastąpiono szeregowymi i odwrotnie.