Kąty trójścienne»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: XXIV OM
- Zadanie pochodzi z artykułu Kąty trójścienne
- Publikacja w Delcie: grudzień 2013
- Publikacja elektroniczna: 01-12-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Dany jest czworościan
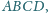 w którym
w którym
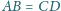 oraz
oraz
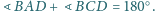 Udowodnij, że
Udowodnij, że
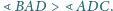
Czy istnieje taki ostrosłup czworokątny
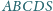 o podstawie
o podstawie
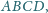 w którym
w którym
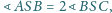
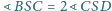 oraz
oraz
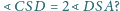

Na rysunku zmodyfikujmy kształty trójkątów tak, aby odpowiednie pary odcinków, które mają się skleić, nadal były równe oraz by przy każdym wierzchołku docelowego czworościanu dowolne dwa kąty płaskie były w sumie większe od trzeciego. Czy te warunki wystarczają, by otrzymać siatkę pewnego czworościanu?
Sfera wpisana w czworościan
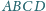 jest styczna do ścian
jest styczna do ścian
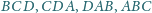 odpowiednio w punktach
odpowiednio w punktach
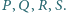 Odcinek
Odcinek
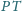 jest średnicą tej sfery, a punkty
jest średnicą tej sfery, a punkty
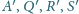 są punktami
przecięcia prostych
są punktami
przecięcia prostych
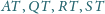 z płaszczyzną
z płaszczyzną
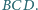 Dowieść,
że punkt
Dowieść,
że punkt
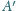 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
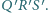
Zwardoń 2002
Zwardoń 2002
Przez środek każdej krawędzi czworościanu prowadzimy płaszczyznę prostopadłą do przeciwległej krawędzi. Wykazać, że istnieje punkt wspólny otrzymanych sześciu płaszczyzn (punkt ten nazywa się punktem Monge’a).
Spodki wysokości pewnego czworościanu są różne od ortocentrów ścian, do których zostały poprowadzone. Wykazać, że płaszczyzny zawierające te wysokości i ortocentra ścian, do których zostały poprowadzone, przecinają się w jednym punkcie.
Zwardoń 2002
Dany jest czworościan
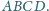 Odcinki
Odcinki
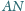 i
i
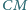 są
dwusiecznymi w trójkącie
są
dwusiecznymi w trójkącie
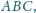 odcinek
odcinek
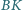 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
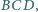 zaś odcinek
zaś odcinek
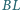 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
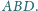 Wykazać, że istnieje punkt wspólny płaszczyzn
Wykazać, że istnieje punkt wspólny płaszczyzn
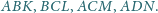
Dany jest czworościan
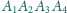 i punkty
i punkty
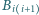 leżące na
krawędziach
leżące na
krawędziach
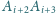 dla
dla
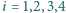 przyjmujemy, że
przyjmujemy, że
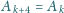 ). Każda z płaszczyzn
). Każda z płaszczyzn
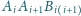 tworzy z płaszczyzną
tworzy z płaszczyzną
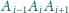 kąt dwuścienny o mierze
kąt dwuścienny o mierze
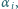 zaś z płaszczyzną
zaś z płaszczyzną
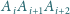 kąt dwuścienny o mierze
kąt dwuścienny o mierze
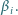 Wykazać, że
płaszczyzny
Wykazać, że
płaszczyzny
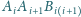 dla
dla
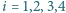 mają wspólny punkt
wtedy i tylko wtedy, gdy
mają wspólny punkt
wtedy i tylko wtedy, gdy
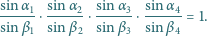 |
Punkt
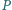 leży wewnątrz czworościanu
leży wewnątrz czworościanu
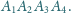 Wykazać, że
płaszczyzny symetryczne do płaszczyzn
Wykazać, że
płaszczyzny symetryczne do płaszczyzn
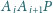 względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
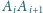 dla
dla
 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
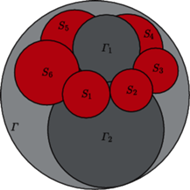
Szare sfery są parami styczne i każda z nich styczna jest do każdej z kolorowych sfer, tworzących łańcuch.
Styczne zewnętrznie sfery
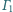 i
i
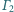 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
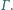 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
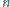 sfer
sfer
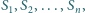 ponadto dla każdego
ponadto dla każdego
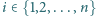 sfera
sfera
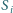 styczna jest do sfery
styczna jest do sfery
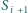 (przy czym
(przy czym
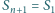 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
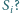 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
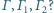 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
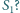
Dany jest czworościan
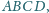 w którym
w którym
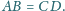 Ponadto
suma pól ścian
Ponadto
suma pól ścian
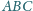 i
i
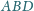 jest równa sumie pól
ścian
jest równa sumie pól
ścian
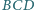 i
i
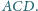 Dowieść, że
Dowieść, że
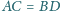 lub
lub
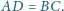
W czworościanie rozważamy dwusieczne trzech kątów płaskich mających wspólny wierzchołek. Wykaż, że jeżeli pewne dwie z tych dwusiecznych są prostopadłe, to wszystkie one są parami prostopadłe.
Zadanie 658 zaproponował pan Tomasz Ordowski.
W przestrzeni dany jest czworościan foremny o krawędzi długości
 oraz dowolny punkt
oraz dowolny punkt
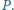 Niech
Niech
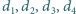 będą
odległościami punktu
będą
odległościami punktu
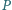 od wierzchołków czworościanu. Wykazać,
że
od wierzchołków czworościanu. Wykazać,
że

Dany jest wielościan wypukły o następujących własnościach: w każdym wierzchołku spotykają się 3 krawędzie, każda ściana jest wielokątem wpisanym w okrąg.
Udowodnić, że każde dwie sąsiednie ściany są wpisane we wspólną, jednoznacznie wyznaczoną sferę.
Dany jest wielościan wypukły o następujących własnościach: w każdym wierzchołku spotykają się 3 krawędzie, każda ściana jest wielokątem wpisanym w okrąg.
Udowodnić, że trzy sąsiednie ściany są wpisane we wspólną sferę.
Dany jest wielościan wypukły o następujących własnościach: w każdym wierzchołku spotykają się 3 krawędzie, każda ściana jest wielokątem wpisanym w okrąg.
Udowodnić, że wielościan jest wpisany w sferę.
W przestrzeni dane są różne punkty
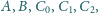 przy czym
przy czym
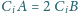 dla
dla
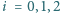 oraz
oraz
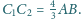 Udowodnij,
że kąt
Udowodnij,
że kąt
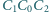 jest prosty i że punkty
jest prosty i że punkty
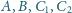 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.
Punkty
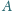 i
i
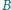 nie należą do płaszczyzny
nie należą do płaszczyzny
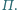 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
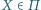 o tej własności, że proste
o tej własności, że proste
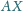 i
i
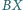 tworzą z płaszczyzną
tworzą z płaszczyzną
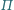 równe kąty.
równe kąty.
Sfera
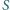 o środku w środku okręgu opisanego na trójkącie
o środku w środku okręgu opisanego na trójkącie
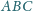 przecina krawędzie
przecina krawędzie
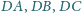 czworościanu
czworościanu
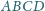 odpowiednio w punktach
odpowiednio w punktach
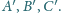 Płaszczyzny styczne
do tej sfery odpowiednio w punktach
Płaszczyzny styczne
do tej sfery odpowiednio w punktach
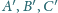 przecinają się w punkcie
przecinają się w punkcie
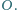 Wykazać, że punkt
Wykazać, że punkt
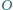 jest środkiem sfery opisanej na
czworościanie
jest środkiem sfery opisanej na
czworościanie
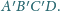
Dany jest ostrosłup
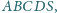 którego podstawą jest czworokąt wypukły
którego podstawą jest czworokąt wypukły
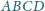 o prostopadłych przekątnych
o prostopadłych przekątnych
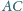 i
i
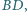 a rzutem
prostokątnym wierzchołka
a rzutem
prostokątnym wierzchołka
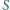 na podstawę jest punkt
na podstawę jest punkt
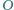 przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
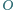 na
ściany boczne ostrosłupa leżą na jednym okręgu.
na
ściany boczne ostrosłupa leżą na jednym okręgu.
Przez wierzchołek
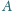 czworościanu
czworościanu
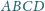 poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
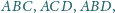 tworzą sześć równych kątów wtedy i tylko wtedy,
gdy
tworzą sześć równych kątów wtedy i tylko wtedy,
gdy

Wykazać, że dla dowolnego czworościanu istnieje trójkąt, którego boki są
równe co do wartości iloczynom przeciwległych krawędzi tego czworościanu.
Wykazać dodatkowo, że pole tego trójkąta jest równe
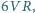 gdzie
gdzie
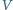 i
i
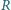 oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
W przestrzeni dany jest skończony zbiór punktów, z których każde cztery są wierzchołkami czworościanu o objętości mniejszej lub równej 1. Wykaż, że istnieje czworościan o objętości nie większej niż 27, zawierający wszystkie te punkty.