Zadanie ZM-1529
o zadaniu...
- Publikacja w Delcie: maj 2017
- Publikacja elektroniczna: 1 maja 2017
Sześcian przecięto płaszczyzną, uzyskując w przekroju pięciokąt opisany na okręgu. Udowodnić, że ten pięciokąt ma oś symetrii.
Sześcian przecięto płaszczyzną, uzyskując w przekroju pięciokąt opisany na okręgu. Udowodnić, że ten pięciokąt ma oś symetrii.
Niech 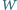 będzie wielościanem wypukłym, środkowo-symetrycznym, i niech
będzie wielościanem wypukłym, środkowo-symetrycznym, i niech 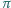 będzie ustaloną płaszczyzną, przechodzącą przez środek symetrii. Przekrój wielościanu
będzie ustaloną płaszczyzną, przechodzącą przez środek symetrii. Przekrój wielościanu 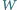 płaszczyzną
płaszczyzną 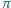 jest zawarty w kole o promieniu
jest zawarty w kole o promieniu 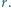 Udowodnić, że przekrój wielościanu
Udowodnić, że przekrój wielościanu 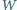 każdą płaszczyzną, równoległą do
każdą płaszczyzną, równoległą do 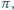 jest zawarty w pewnym kole o promieniu
jest zawarty w pewnym kole o promieniu  - lub podać przykład, pokazujący nieprawdziwość takiego stwierdzenia.
- lub podać przykład, pokazujący nieprawdziwość takiego stwierdzenia.
Czy w sześcianie o krawędzi 20 zmieści się kwadrat o boku 21?
Czy w sześcianie o krawędzi 20 można wywiercić tunel, przez który da się przesunąć sześcian o krawędzi 21?
Wierzchołek czworościanu nazwijmy ciekawym, jeśli z trzech wychodzących zeń krawędzi nie da się zbudować trójkąta.
Czy z prostopadłościennych klocków o wymiarach 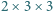 można ułożyć prostopadłościan o wymiarach
można ułożyć prostopadłościan o wymiarach 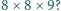
Z kostek domina o wymiarach 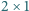 ułożono szachownicę
ułożono szachownicę 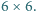 Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Z klocków o wymiarach 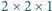 zbudowano sześcian
zbudowano sześcian 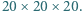 Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.
Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.
Klockiem nazwiemy bryłę otrzymaną przez usunięcie z sześcianu o krawędzi 2 jednego spośród ośmiu sześcianów jednostkowych, z których jest on zbudowany. Udowodnij, że po usunięciu z sześcianu o krawędzi 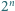 dowolnego spośród
dowolnego spośród 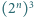 tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami.
tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami.
Zadanie 1 pochodzi z gazetki Olimpiady Matematycznej Gimnazjalistów Kwadrat nr 7
W trapezie 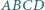 podstawa
podstawa 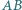 ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt
ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt 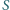 jest wierzchołkiem ostrosłupa o podstawie
jest wierzchołkiem ostrosłupa o podstawie 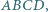 w którym
w którym 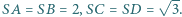 Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.
Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.
Dany jest ostrosłup prawidłowy czworokątny, którego każda krawędź ma długość 1. Ostrosłup ten przecięto płaszczyzną przecinającą jego wszystkie krawędzie boczne i uzyskano w przekroju czworokąt wypukły 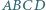 nie będący trapezem. Proste
nie będący trapezem. Proste 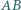 i
i 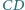 przecinają się w punkcie
przecinają się w punkcie 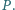 Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu
Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu 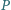 od płaszczyzny podstawy ostrosłupa.
od płaszczyzny podstawy ostrosłupa.
Dany jest sześcian o podstawie 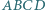 i krawędziach bocznych
i krawędziach bocznych 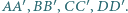 Wyznacz miarę kąta dwuściennego między płaszczyznami
Wyznacz miarę kąta dwuściennego między płaszczyznami 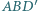 i
i 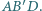
Dwie spośród ścian pewnego wielościanu są przystającymi wielokątami położonymi w równoległych płaszczyznach, przy czym jedną z nich można tak przesunąć, by uzyskać drugą. Wszystkie pozostałe ściany tego wielościanu są równoległobokami. Czy wynika z tego, że rozważany wielościan jest graniastosłupem?
Czy istnieje wielościan o 333 ścianach, z których każda jest trójkątem?
Czy istnieje wielościan o 7 krawędziach?
Czy istnieje wielościan wypukły mający 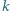 krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca
krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca  krawędzi, przy czym
krawędzi, przy czym 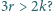
Czy istnieje wielościan wypukły, w którym 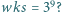
Udowodnij, że w każdym wielościanie wypukłym 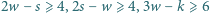 oraz
oraz 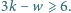
Zadanie 6 pochodzi z Ligi Zadaniowej Olimpiady Matematycznej Gimnazjalistów.
Pewien wielościan wypukły ma 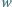 wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
Udowodnij, że każdy wielościan wypukły ma ścianę trójkątną lub naroże trójścienne.
Wykaż, że w każdym wielościanie wypukłym suma liczby ścian trójkątnych i liczby naroży trójściennych jest większa lub równa 8.
Krawiec ma worek płaskich pięciokątów foremnych o boku 1 oraz worek płaskich sześciokątów foremnych o boku 1. Jakie wielościany wypukłe może z nich uszyć?
Jakie istnieją wielościany foremne wypukłe?
Czy istnieje wielościan wypukły o czworokątnych ścianach i o 25 krawędziach?
Wykaż, że każdy wielościan wypukły ma wierzchołek o mniej niż 6 krawędziach oraz ścianę o mniej niż 6 bokach.
Na sferze o promieniu 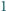 dana jest krzywa zamknięta o długości mniejszej niż
dana jest krzywa zamknięta o długości mniejszej niż 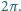 Wykazać, że ta krzywa jest zawarta w pewnej półsferze.
Wykazać, że ta krzywa jest zawarta w pewnej półsferze.
Czy istnieje taki ostrosłup 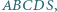 którego podstawą jest prostokąt
którego podstawą jest prostokąt 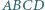 i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość
i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość 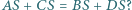 Odpowiedź uzasadnij.
Odpowiedź uzasadnij.
Czy istnieje przekrój dwudziestościanu foremnego płaszczyzną przechodzącą przez jego środek, będący jedenastokątem?