Zadanie ZM-19.06-KPO-2
o zadaniu...
- Publikacja w Delcie: czerwiec 2019
- Publikacja elektroniczna: 31 maja 2019
Dany jest czworościan 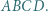 Punkt
Punkt 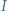 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 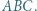 Punkt
Punkt 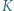 leży na odcinku
leży na odcinku 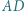 i spełnia warunek
i spełnia warunek

Proste 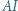 i
i 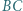 przecinają się w punkcie
przecinają się w punkcie 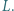 Dowieść, że prosta
Dowieść, że prosta 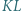 przechodzi przez środek odcinka
przechodzi przez środek odcinka 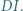

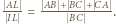 Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta
Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta 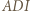 i prostej
i prostej