Czego jeszcze nie wiedzieliśmy o bryłach platońskich?
"Bryły platońskie" to inna nazwa wielościanów foremnych. W przestrzeni trójwymiarowej jest ich dokładnie 5 i są to: czworościan, sześcian, ośmiościan, dwunastościan oraz dwudziestościan foremny. Ich historia sięga czasów starożytnych i wydawałoby się, że po ponad dwóch tysiącach lat wiemy o nich już absolutnie wszystko.
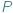 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 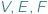 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 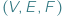 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości: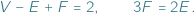

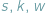 ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego
ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 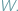 Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
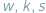 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 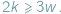 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 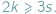 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: 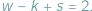

 i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).