Zadanie ZM-1541
o zadaniu...
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
Trójkąt prostokątny 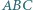 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 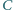 obrócono wokół prostej
obrócono wokół prostej 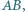 otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg
otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg  Sfera
Sfera 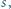 do której należy punkt
do której należy punkt 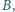 jest styczna do sfery
jest styczna do sfery 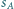 o środku
o środku 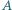 i promieniu
i promieniu 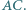 Sfery
Sfery 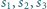 są styczne do sfery
są styczne do sfery  oraz do sfery
oraz do sfery 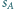 w pewnych punktach należących do okręgu
w pewnych punktach należących do okręgu 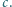 Udowodnić, że sfery
Udowodnić, że sfery 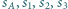 mają wspólną płaszczyznę styczną.
mają wspólną płaszczyznę styczną.

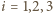 oznaczmy przez
oznaczmy przez 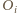 środek sfery
środek sfery 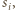 a przez
a przez 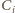 - punkt styczności sfery
- punkt styczności sfery 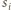 ze sferą
ze sferą 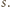 Ponieważ
Ponieważ 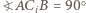 oraz punkty
oraz punkty 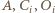 są współliniowe, więc również
są współliniowe, więc również 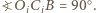
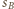 o środku
o środku 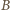 i promieniu
i promieniu 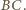 Dla
Dla 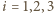 sfera
sfera 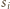 jest prostopadła do sfery
jest prostopadła do sfery 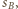 więc jest zachowywana przy rozważanej inwersji. Tę samą własność ma sfera
więc jest zachowywana przy rozważanej inwersji. Tę samą własność ma sfera 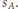 Wobec tego obrazem sfery
Wobec tego obrazem sfery  (przechodzącej przez środek inwersji) jest pewna płaszczyzna, która jest styczna do
(przechodzącej przez środek inwersji) jest pewna płaszczyzna, która jest styczna do