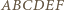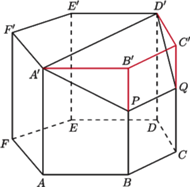
Tak, taki wielościan istnieje. Rozpatrzmy graniastosłup sześciokątny o podstawach oraz 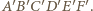Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt 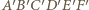można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. 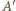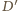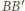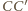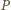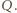Poprowadźmy więc przez punkty oraz płaszczyznę przecinającą krawędzie i odpowiednio w punktach oraz Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma 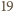krawędzi.

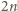Czytelnik Uważny skonstruuje podobną metodą inne przykłady wielościanów o zadanych własnościach, rozpatrując graniastosłup o podstawie będącej -kątem, dla