Postaw na krawędzi!»Zadanie 3
o zadaniu...
- Zadanie olimpijskie: XLIV OM.
- Zadanie pochodzi z artykułu Postaw na krawędzi!
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (51 KB)
Rozstrzygnij, czy można obliczyć objętość czworościanu, znając pola jego czterech ścian oraz promień kuli opisanej.
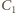i
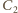wpisane
odpowiednio w prostopadłościany o wymiarach
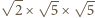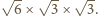
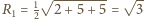oraz
oraz
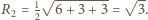
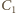jest
trójkątem o bokach
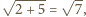
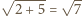oraz
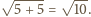Wysokość takiego trójkąta, opuszczona na bok
o długości
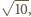równa jest
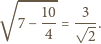
równe jest
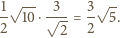
też równe jest
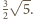
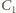i
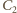mają więc równe pola ścian
i promienie kul opisanych. Tymczasem ich objętości są różne:
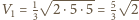oraz
