Postaw na krawędzi!»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: XLII OM
- Zadanie pochodzi z artykułu Postaw na krawędzi!
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (51 KB)
Czy istnieją czworościany
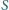 i
i
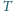 o następujących dwóch
własnościach:
o następujących dwóch
własnościach:
- a)
- objętość czworościanu
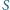 jest większa od objętości
czworościanu
jest większa od objętości
czworościanu
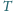 ;
;
- b)
- pole każdej ściany czworościanu
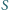 nie przekracza pola
żadnej ściany czworościanu
nie przekracza pola
żadnej ściany czworościanu
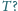

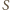 zbudujemy czworościan
zbudujemy czworościan
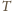 o żądanych własnościach. Niech
o żądanych własnościach. Niech
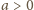 będzie taką liczbą, aby
liczba
będzie taką liczbą, aby
liczba
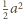 była większa od pola każdej ściany czworościanu
była większa od pola każdej ściany czworościanu
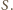 Niech
Niech
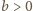 będzie taką liczbą, aby liczba
będzie taką liczbą, aby liczba
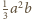 była
mniejsza od objętości czworościanu
była
mniejsza od objętości czworościanu
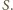
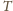 będzie czworościanem wpisanym w prostopadłościan
o podstawie
będzie czworościanem wpisanym w prostopadłościan
o podstawie
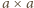 i wysokości
i wysokości
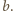 Objętość
Objętość
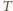 równa
jest
równa
jest
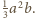 Każdą ścianę czworościanu
Każdą ścianę czworościanu
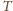 można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
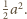 Z definicji liczb
Z definicji liczb
 i
i
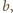 czworościany
czworościany
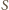 i
i
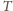 spełniają żądane warunki.
spełniają żądane warunki.