Klub 44M - zadania V 2017»Zadanie 741
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2017
- Publikacja w Delcie: maj 2017
- Publikacja elektroniczna: 1 maja 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (82 KB)
Niech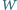 
będzie wielościanem wypukłym, środkowo-symetrycznym, i niech 
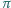będzie ustaloną płaszczyzną, przechodzącą przez środek symetrii. Przekrój wielościanu 
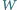płaszczyzną 
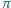jest zawarty w kole o promieniu 
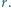Udowodnić, że przekrój wielościanu 
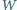każdą płaszczyzną, równoległą do 
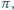jest zawarty w pewnym kole o promieniu 
- lub podać przykład, pokazujący nieprawdziwość takiego stwierdzenia.
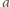). Weźmy jego dwa przeciwległe wierzchołki 
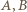(końce przekątnej długości 
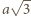). Płaszczyzna 
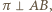przechodząca przez środek 
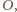tworzy w przecięciu z sześcianem sześciokąt foremny, którego wierzchołkami są środki niektórych krawędzi sześcianu, leżące w odległości 
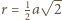od środka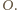 
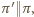przechodzącą przez trzy wierzchołki (połączone krawędziami np. z punktem 
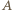) jest trójkątem foremnym o boku 
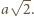Najmniejsze koło, zawierające ów trójkąt, ma promień 