Łuki Talesa»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Łuki Talesa
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
-
Zadanie 4 jest modyfikacją zadania z XXV Olimpiady Matematycznej. Więcej o nim m.in. w Delcie 5/1986.
W czworościanie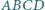 
krawędź 
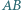jest prostopadła do krawędzi 
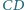i 
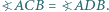Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź 
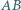i środek krawędzi 
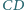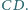
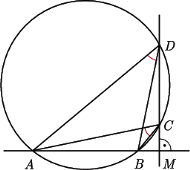
jest prostopadła do krawędz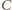i 
i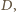 
a więc też trójkąty 
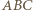i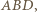 
są symetryczne względem opisanej płaszczyzny, zatem przystające. Wykażemy, że tak być nie musi.
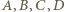leżą na jednym okręgu w tej właśnie kolejności, przy czym 
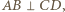a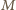 
to punkt przecięcia tych prostych. Wówczas trójkąty 
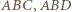nie są przystające (mają różne wysokości na 
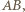więc też różne pola). Jednocześnie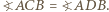 
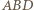wokół prostej 
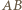o pewien dodatni kąt mniejszy od 
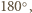otrzymamy czworościan 
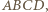w którym 
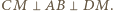Wobec tego prosta 
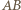jest prostopadła do płaszczyzny 
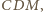a więc także do każdej prostej zawartej w tej płaszczyźnie. Stąd 
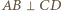także po opisanym obrocie. Uzyskaliśmy więc czworościan 
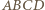spełniający warunki zadania, w którym trójkąty 
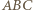i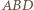 
nie są przystające.