X Olimpiada Matematyczna Gimnazjalistów»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: II OMG
- Zadanie pochodzi z artykułu X Olimpiada Matematyczna Gimnazjalistów
- Publikacja w Delcie: lipiec 2015
- Publikacja elektroniczna: 30-06-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (176 KB)
Czy istnieje taki ostrosłup czworokątny, którego każda ściana boczna jest trójkątem prostokątnym?
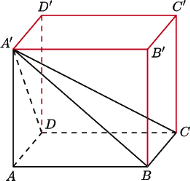
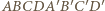będzie prostopadłościanem. Wówczas ostrosłup 
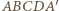spełnia warunki zadania.
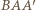oraz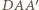 
są, oczywiście, prostokątne. Ponadto, ponieważ prosta 
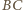jest prostopadła do płaszczyzny 
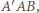to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej 
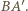Zatem trójkąt 
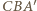jest prostokątny. Podobnie dowodzimy, że trójkąt 
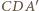jest prostokątny.