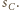Zadanie ZM-1531
o zadaniu...
- Publikacja w Delcie: czerwiec 2017
- Publikacja elektroniczna: 31 maja 2017
Punkty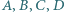 
są takimi czterema wierzchołkami pewnego prostopadłościanu, że żadne dwa z nich nie są połączone krawędzią. Sfery 
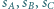o środkach odpowiednio w punktach 
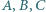są parami styczne. Udowodnić, że istnieje sfera 
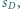o środku w punkcie 
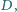która jest styczna do sfer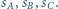 
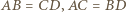oraz 
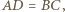gdyż są to pary przekątnych przystających prostokątów.
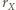promień sfery 
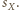Jeżeli sfery 
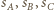są parami styczne, to pewne dwie z nich - bez straty ogólnośc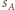i 
i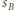 
- są styczne zewnętrznie, czyli 
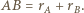Jeśli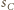 
jest styczna zewnętrznie do 
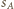i 
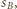to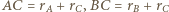 
i wystarczy przyjąć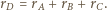
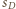będzie styczna wewnętrznie do pozostałych trzech sfer, gdyż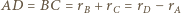
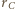jest styczna wewnętrznie do 
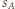i 
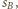to
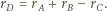
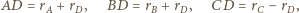
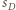będzie styczna zewnętrznie do 
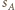i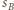 
oraz styczna wewnętrznie do 