Klub 44M - zadania II 2019»Zadanie 776
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2019
- Publikacja w Delcie: luty 2019
- Publikacja elektroniczna: 1 lutego 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (550 KB)
-
Zadanie 776 zaproponował pan Adam Woryna.
Sześcian o krawędzi długości 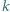 przecinamy płaszczyzną
przecinamy płaszczyzną 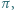 położoną w odległości
położoną w odległości 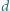 od środka sześcianu. Jaka jest maksymalna wartość
od środka sześcianu. Jaka jest maksymalna wartość 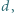 przy której płaszczyzna
przy której płaszczyzna 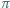 może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?
może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?

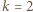 i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty
i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty 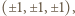 a rzutem prostokątnym punktu
a rzutem prostokątnym punktu 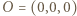 na płaszczyznę
na płaszczyznę 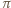 jest punkt
jest punkt 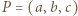 o współrzędnych
o współrzędnych 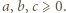 Zatem
Zatem 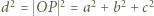 ; zaś płaszczyzna
; zaś płaszczyzna 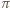 jest dana równaniem
jest dana równaniem 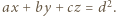
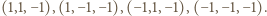 Każda z półprzestrzeni (
Każda z półprzestrzeni ( 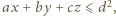
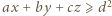 ) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność
) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność 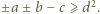 Skoro
Skoro 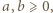 znaczy to, że
znaczy to, że 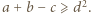
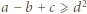 oraz
oraz 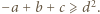 Dodajemy te trzy nierówności i otrzymujemy
Dodajemy te trzy nierówności i otrzymujemy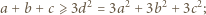
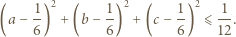
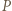 od punktu
od punktu 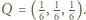 Tak więc
Tak więc 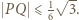 A ponieważ
A ponieważ 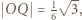 ostatecznie
ostatecznie 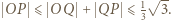
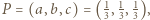 wszystkie nierówności stają się równościami; płaszczyzna o równaniu
wszystkie nierówności stają się równościami; płaszczyzna o równaniu 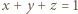 leży w odległości
leży w odległości 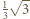 od
od 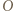 i spotyka wszystkie ściany. Dla
i spotyka wszystkie ściany. Dla 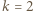 szukane maksimum wynosi więc
szukane maksimum wynosi więc 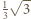 ; zaś w przypadku ogólnym - po przeskalowaniu - wynosi
; zaś w przypadku ogólnym - po przeskalowaniu - wynosi