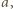(a) Weźmy dowolny czworościan oraz jego najdłuższą krawędź. Przyjmijmy, że ma ona długość zaś dwie przyległe do niej ściany mają krawędzie długości 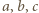oraz 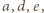przy czym krawędzie 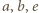mają wspólny koniec oraz krawędzie 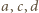mają wspólny koniec. Wówczas 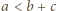oraz 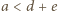; stąd 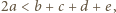wobec czego musi zachodzić co najmniej jedna z nierówności 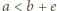lub 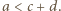Zatem co najmniej jeden z końców krawędzi nie jest wierzchołkiem ciekawym.

(b) Dokładnie jeden wierzchołek ciekawy jest możliwy. Rozpocznijmy od przykładu czworościanu zdegenerowanego do czwórki punktów na płaszczyźnie w konfiguracji: - trójkąt prostokątny; - środek przeciwprostokątnej 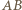; 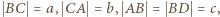przy czym 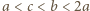(np. 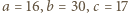). Z punktu 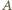wychodzą krawędzie długości 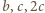; z punktu 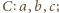z punktu 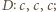każda z tych trójek spełnia warunek trójkąta. Pozostaje wierzchołek 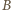- jedyny ciekawy (wspólny koniec krawędzi 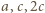). Teraz wystarczy wyjść w przestrzeń i nieznacznie przemieścić wierzchołek 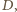usuwając go prostopadle z płaszczyzny 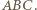Wychodzące zeń krawędzie trochę się wydłużą. Przy małym przemieszczeniu rozważane nierówności (ostre) pozostaną w mocy; punkt nadal będzie jedynym wierzchołkiem ciekawym.