Klub 44M - zadania X 2014»Zadanie 688
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2014
- Publikacja w Delcie: październik 2014
- Publikacja elektroniczna: 1 października 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (66 KB)
-
Zadanie 688 zaproponował pan Witold Bednarek z Łodzi.
Trójkąt równoboczny 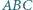 o boku długości 1 jest podstawą ostrosłupa prawidłowego
o boku długości 1 jest podstawą ostrosłupa prawidłowego 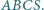 Na krawędziach
Na krawędziach 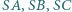 leżą takie punkty
leżą takie punkty 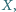
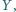
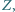 że suma kwadratów pól trójkątów
że suma kwadratów pól trójkątów  jest równa kwadratowi pola trójkąta
jest równa kwadratowi pola trójkąta 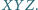 Obliczyć objętość ostrosłupa
Obliczyć objętość ostrosłupa 

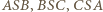 są przystającymi trójkątami równoramiennymi, z jednakowym kątem
są przystającymi trójkątami równoramiennymi, z jednakowym kątem 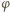 przy wierzchołku
przy wierzchołku 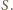 Niech
Niech 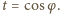 Oznaczając
Oznaczając 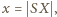
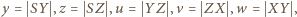 mamy
mamy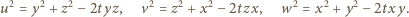
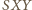 wynosi
wynosi 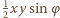 ; podobnie wyrażają się pola trójkątów
; podobnie wyrażają się pola trójkątów 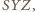
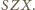 Suma kwadratów ich pól jest równa
Suma kwadratów ich pól jest równa 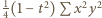 ; tu i dalej symbol
; tu i dalej symbol 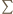 oznacza sumę cykliczną względem trójki
oznacza sumę cykliczną względem trójki 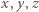 (lub
(lub 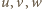 ).
). wyrażamy zgodnie ze wzorem Herona jako
wyrażamy zgodnie ze wzorem Herona jako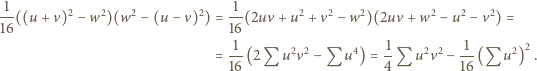
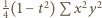 ; mnożąc przez 4 dostajemy równanie
; mnożąc przez 4 dostajemy równanie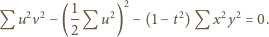
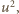
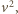
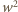 wyrażeń (1) i pogrupowaniu wszystkiego według potęg
wyrażeń (1) i pogrupowaniu wszystkiego według potęg 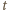 (to mechaniczny rachunek) okazuje się, że wyrazy niezawierające
(to mechaniczny rachunek) okazuje się, że wyrazy niezawierające 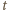 znoszą się, a całe równanie (2) redukuje się do postaci
znoszą się, a całe równanie (2) redukuje się do postaci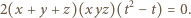
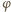 jest niezerowy, więc
jest niezerowy, więc 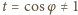 ; stąd
; stąd 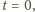 czyli
czyli 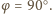 Zatem każdy z trójkątów
Zatem każdy z trójkątów 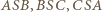 jest prostokątny i równoramienny, o przeciwprostokątnej długości 1; przyprostokątne
jest prostokątny i równoramienny, o przeciwprostokątnej długości 1; przyprostokątne 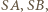
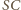 mają długość
mają długość 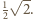 Ostrosłup
Ostrosłup 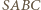 jest szóstą częścią sześcianu o krawędzi
jest szóstą częścią sześcianu o krawędzi 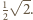 Jego objętość wynosi
Jego objętość wynosi