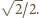Przecięcia płaszczyzn»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: III Olimpiada Matematyczna Gimnazjalistów
- Zadanie pochodzi z artykułu Przecięcia płaszczyzn
- Publikacja w Delcie: sierpień 2016
- Publikacja elektroniczna: 31 lipca 2016
Dany jest ostrosłup prawidłowy czworokątny, którego każda krawędź ma długość 1. Ostrosłup ten przecięto płaszczyzną przecinającą jego wszystkie krawędzie boczne i uzyskano w przekroju czworokąt wypukły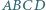 
nie będący trapezem. Proste 
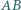i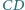 
przecinają się w punkcie 
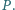Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu 
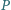od płaszczyzny podstawy ostrosłupa.
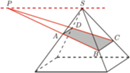
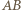leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta 
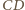w płaszczyźnie tylnej ściany, więc punkt 
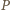należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek 
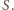Stąd jedyną wartością, jaką może przyjąć odległość punktu 
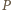od płaszczyzny podstawy, jest wysokość ostrosłupa równa 