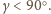Kąty trójścienne»Zadanie 3
o zadaniu...
- Zadanie olimpijskie: XXVIII OM
- Zadanie pochodzi z artykułu Kąty trójścienne
- Publikacja w Delcie: grudzień 2013
- Publikacja elektroniczna: 01-12-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Udowodnij, że w każdym czworościanie istnieje wierzchołek, przy którym trzy kąty płaskie są ostre.
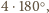jako
suma kątów czterech trójkątów. Wobec tego istnieje taki wierzchołek
czworościanu, przy którym suma trzech kątów płaskich nie przekracza
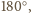w przeciwnym razie suma wszystkich kątów płaskich czworościanu
przekraczałaby
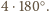
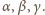Wówczas
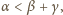więc
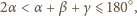
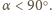Analogicznie
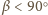oraz
