Stereometria Kącik przestrzenny
-
-
Stereometria Kącik przestrzenny
Inwersja w przestrzeni i rzut stereograficzny
Kiedy na płaszczyźnie mamy do czynienia z okręgami, to bardzo często posługujemy się rachunkiem na kątach, ponieważ znamy wiele przydatnych twierdzeń i faktów z tego zakresu. Niestety, trudno o analogiczne narzędzia w przestrzeni. Stanowi to wielki kłopot, gdy zmagamy się z zadaniami o sferach. Istnieje jednak kilka innych technik, skutecznych w zadaniach o okręgach, które działają również w przestrzeni. Są to: potęga punktu, jednokładność oraz inwersja. O tej ostatniej metodzie opowiemy w tym kąciku.
-

Geometria jest nauką doświadczalną
W wielu miejscach można przeczytać czy usłyszeć, że matematyka, a zwłaszcza geometria jest nauką aksjomatyczną i wszelkie zawarte w niej fakty uzyskuje się właśnie z aksjomatów przez podporządkowane prawom logiki dowody.
-
Lekcja 3 - Sześcioośmiościan
W wielu rysunkach bardzo pomocny jest sześcian, z narysowaniem którego raczej nie mamy problemu...
-
Okręgi wielkie
Którędy przebiega najkrótsza droga lotnicza z Warszawy do Vancouveru? Wbrew pozorom – mimo podobnej szerokości geograficznej – wcale nie wzdłuż równoleżnika, a nad Grenlandią, o czym łatwo się przekonać, naciągając nitkę na globusie.
-
Stereometria Kącik przestrzenny
Czworościany równościenne - część II
Kontynuujemy opowieść o czworościanach równościennych – tym razem przyjrzymy się paru zadaniom z nimi związanym. Jakiś czas temu na konkursach matematycznych temat tych wdzięcznych czworościanów był dosyć modny...
-
Stereometria Stowarzyszenie na rzecz Edukacji Matematycznej
Wszystko może się przydać
Panuje przekonanie, że w nauczaniu matematyki powinno się eksponować fakt, że ma ona zastosowania. Gdy przyjrzeć się podręcznikom, a zwłaszcza testom kwalifikacyjnym, trudno oprzeć się wrażeniu, że są to rzeczy w stylu mierzenia wysokości piramidy za pomocą długości jej cienia i twierdzenia Talesa, lub też zadań w stylu: jeśli dwóch robotników kopie rów w ciągu 2 godzin, to ilu ich potrzeba, aby ten rów wykopać w 15 sekund? (odpowiedź: 1440).
-
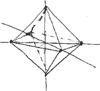
Lekcja 2 - ośmiościan
Kontynuujemy lekcje rysunku rozpoczęte w Delcie 6/2012. Kolejnym obiektem, który będziemy rysować, jest ośmiościan.
-
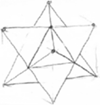
Lekcja 1 - Stella octangula
Wydaje się, że w czasach szybkich komputerów, programów graficznych i innych gadżetów nie ma sensu zajmowanie się rysunkiem odręcznym. Równie dobrze jednak można by zrezygnować z nauki pisania i tabliczki mnożenia – są przecież odpowiednie edytory i kalkulatory. Zdarza się jednak, że rozwiązując jakieś zadanie, dobrze byłoby podeprzeć naszą wyobraźnię właśnie rysunkiem, a nie ma pod ręką supernowoczesnych narzędzi.
-
Stereometria Stowarzyszenie na rzecz Edukacji Matematycznej
O LXIII Olimpiadzie Matematycznej
W zawodach I stopnia obecnej, LXIII Olimpiady Matematycznej wzięło udział 1409 uczniów, więc nieco mniej niż w poprzedniej. Jest to liczba bliska wieloletniej średniej. Do drugiego stopnia zakwalifikowano 622 uczniów. Zawody drugiego stopnia odbyły się 17 i 18 lutego.
-
Kwadrat, którego nie ma
Przemieszczając się na płaszczyźnie za pomocą ruchów „do przodu”, „do tyłu”, „w lewo” i „w prawo”, możemy w szczególności narysować kwadrat. Czy analogiczna sytuacja rozważana na zakrzywionej powierzchni zawsze pozwala na wygenerowanie kwadratu przez zakreślaną trajektorię? Rozważmy sferę, którą często wykorzystuje się w globalnym modelowaniu powierzchni Ziemi.
-
O czworościanie równościennym
Czy istnieje czworościan który nie jest foremny, a którego ściany są trójkątami przystającymi? Istnieje...
-
Stereometria Kącik przestrzenny
Czworościany równościenne – część I
Na płaszczyźnie, jeśli trójkąt ma równe boki, to jest równoboczny. W przestrzeni jednak czworościan, którego ściany są przystające, wcale nie musi być foremny...
-
Odkryj twierdzenie sam
Czasem przydaje się do czegoś twierdzenie o dwusiecznej...
-
Jak zrobić fleksagon?
Fleksagony to rodzina figur, które odpowiednio złożone z płaskiej kartki papieru mogą wskutek obracania pokazać nam cztery lub więcej „twarzy” (zamiast dwóch).
-
Stereometria Kącik przestrzenny
Jak wyjść z dżungli?
Każdy, kto był w dżungli lub chociaż widział ją w jakimś filmie, wie, że poruszanie się po niej jest, delikatnie mówiąc, dosyć uciążliwe. Stanowi to ogromny kłopot szczególnie wtedy, gdy ktoś się w niej zgubi i chce się jakoś wydostać. Nie dość, że nie wiadomo, w jakim kierunku iść, to w ogóle ciężko jest nam pokonywać przeszkody (a rozwiązania siłowe, takie jak maczeta, niewiele dają). Istnieje następujące zalecenie: wystarczy znaleźć strumień (co zresztą wcale nie musi być łatwe), a potem liczyć na to, że zaprowadzi nas on do większej rzeki, a ta, być może, do morza.
-
Stereometria Kącik przestrzenny
Trzy rozwiązania pewnego zadania
W tym kąciku zajmiemy się pewnym zadaniem o czworościanie foremnym, o którym, między innymi, miałem okazję opowiadać na XLVI Szkole Matematyki Poglądowej pod hasłem Podejście niestandardowe.
-
Stereometria Doświadczenia myślowe
O wieszaniu bombek na choince
Święta za pasem, więc przygotujmy się nieco do wieszania bombek na choince.
-
Siatki, grafy, wielościany
-
Stereometria Kącik przestrzenny
Kąty dwuścienne
W tym odcinku przyjrzymy się kątom dwuściennym. Jedną z najbardziej skutecznych metod radzenia sobie z nimi jest przeformułowanie problemu tak, żeby zamiast kątów dwuściennych pojawiły się kąty płaskie.
-
Stereometria Kącik przestrzenny
Kąty płaskie w przestrzeni
Tym razem opowiemy o kątach w przestrzeni, a dokładniej o tym, jak rozwiązywać zadania zawierające nierówności miar kątów w przestrzeni. W zadaniach pojawiają się dwa typy kątów – płaskie i dwuścienne. Ten odcinek poświęcimy kątom płaskim, a o dwuściennych opowiemy następnym razem.
-
Numerowanie
Na pierwszym etapie tegorocznej Olimpiady Matematycznej pojawiło się poniższe zadanie 1 o numerowaniu krawędzi dwunastościanu. Spośród licznych zadań o podobnej tematyce prezentujemy kilka o dość różnorodnych rozwiązaniach.
-
Stereometria Stowarzyszenie na rzecz Edukacji Matematycznej
Czworościan i kule
W dniu 8 stycznia 2011 roku odbyły się zawody II stopnia VI Olimpiady Matematycznej Gimnazjalistów, w których uczestniczyło 669 uczniów. Spośród nich 187 zostało zakwalifikowanych do zawodów stopnia III.
-
Wielościan o siedmiu krawędziach i jego znajomi
Dla każdej liczby naturalnej
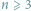 można, oczywiście, narysować wielokąt,
który ma
można, oczywiście, narysować wielokąt,
który ma
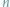 boków. A jak to będzie z wielościanami o zadanej z góry liczbie
krawędzi?
boków. A jak to będzie z wielościanami o zadanej z góry liczbie
krawędzi?
-
Stereometria Kącik przestrzenny
Zejdźmy na ziemię
Czasami, gdy zbytnio bujamy w obłokach, słyszymy od innych zejdź na ziemię! Kto by pomyślał, że ta zazwyczaj dość nieprzyjemna uwaga może być niekiedy cenną wskazówką do zadań ze stereometrii.