Kąty trójścienne»Zadanie 5
o zadaniu...
- Zadanie olimpijskie: OM LXIV
- Zadanie pochodzi z artykułu Kąty trójścienne
- Publikacja w Delcie: grudzień 2013
- Publikacja elektroniczna: 01-12-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Dany jest czworościan
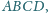w którym
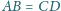oraz
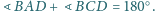Udowodnij, że
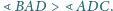
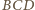danego czworościanu wokół krawędzi
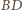tak, aby znalazła się w płaszczyźnie ściany
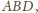ale po
przeciwnej stronie prostej
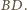Na uzyskanym w ten sposób czworokącie
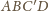można opisać okrąg, gdyż
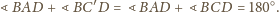
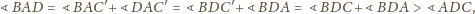
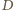czworościanu. To kończy dowód.