Mała Delta
O tym, czego nie ma
Wielościan o siedmiu krawędziach i jego znajomi
Dla każdej liczby naturalnej
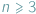 można, oczywiście, narysować
wielokąt, który ma
można, oczywiście, narysować
wielokąt, który ma
 boków. A jak to będzie z wielościanami
o zadanej z góry liczbie krawędzi?
boków. A jak to będzie z wielościanami
o zadanej z góry liczbie krawędzi?
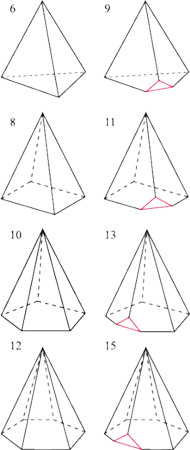
Rys. 1
Po pierwsze, nie uda się nikomu skonstruować wielościanu o
 krawędziach
dla
krawędziach
dla
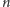 ze zbioru
ze zbioru
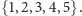 Wielościan bowiem musi mieć
przynajmniej cztery wierzchołki (trzy to jeszcze za mało, bo trzy punkty zawsze
leżą w jednej płaszczyźnie), a z każdego wierzchołka wychodzić muszą
przynajmniej trzy krawędzie. Ponieważ każda krawędź łączy ze sobą dwa
wierzchołki, to krawędzi musi być przynajmniej
Wielościan bowiem musi mieć
przynajmniej cztery wierzchołki (trzy to jeszcze za mało, bo trzy punkty zawsze
leżą w jednej płaszczyźnie), a z każdego wierzchołka wychodzić muszą
przynajmniej trzy krawędzie. Ponieważ każda krawędź łączy ze sobą dwa
wierzchołki, to krawędzi musi być przynajmniej
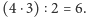 Pięć albo
mniej – to jeszcze za mało.
Pięć albo
mniej – to jeszcze za mało.
Wielościan o sześciu krawędziach, oczywiście, istnieje: to czworościan.
Nietrudno także jest wskazać wielościany o
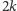 krawędziach dla
krawędziach dla
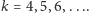 Będą to ostrosłupy o podstawie czworokąta, pięciokąta,
sześciokąta, … (patrz Rys. 1 (lewa kolumna)).
Będą to ostrosłupy o podstawie czworokąta, pięciokąta,
sześciokąta, … (patrz Rys. 1 (lewa kolumna)).
Skonstruujemy teraz serię wielościanów o nieparzystej liczbie krawędzi równej odpowiednio 9, 11, 13, …. Wystarczy każdemu z ostrosłupów z rysunku 1 tak obciąć rożek przy podstawie, jak pokazuje to rysunek 2 (prawa kolumna). Przybędą wtedy trzy nowe krawędzie (jedna na każdej ścianie przy odcinanym rożku).

Rys. 2 Gdy płaszczyznę cięcia prowadzimy równolegle do ustalonej krawędzi wielościanu i niedaleko od niej, to na przekroju otrzymujemy wielokąt, który ma przynajmniej dwa boki równoległe.
Ile by się kto nie męczył, nie uda mu się do katalogu z rysunków 1 i 2
dołożyć wielościanu o siedmiu krawędziach. Gdyby bowiem taki wielościan
istniał, to miałby przynajmniej pięć wierzchołków (wielościan o czterech
wierzchołkach to czworościan, który ma sześć krawędzi). Z każdego
wierzchołka wychodzą przynajmniej 3 krawędzie, każda łączy dwa wierzchołki,
więc nasz wielościan miałby krawędzi przynajmniej
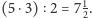 To sprzeczność, która dowodzi, że wielościanu o siedmiu krawędziach
nie ma.
To sprzeczność, która dowodzi, że wielościanu o siedmiu krawędziach
nie ma.
Rozumując tak samo można udowodnić, że nie ma wielościanu o nieparzystej liczbie ścian, z których każda jest trójkątem.
Nie ma także wielościanu wypukłego, w którym każda ściana byłaby
wielokątem o innej liczbie boków. Gdyby bowiem istniał, to wybralibyśmy
ścianę o największej liczbie boków, powiedzmy
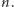 Przylegałoby do niej
Przylegałoby do niej
 innych ścian, każda o innej liczbie boków, nie mniejszej
niż 3 i nie większej niż
innych ścian, każda o innej liczbie boków, nie mniejszej
niż 3 i nie większej niż
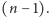 Takich ścian może być jednak
co najwyżej
Takich ścian może być jednak
co najwyżej
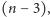 sprzeczność.
sprzeczność.
Na koniec udowodnimy, że nie ma wielościanu, którego każdy przekrój byłby trójkątem. Ustalmy dowolną krawędź wielościanu i tak poprowadźmy płaszczyznę przekroju, by była do tej krawędzi równoległa i w dodatku przecinała obie przylegające do niej ściany (Rys. 2). Na przekroju powstanie wielokąt o dwóch bokach równoległych – nie będzie to więc trójkąt.
Jeszcze i innych nieistniejących znajomych wielościanu o siedmiu krawędziach można wymyśleć wielu. Polecamy tę pouczającą zabawę.