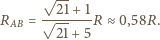Klub 44F - zadania VI 2005»Zadanie 401
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania VI 2005
- Publikacja w Delcie: czerwiec 2005
- Publikacja elektroniczna: 24 sierpnia 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (76 KB)
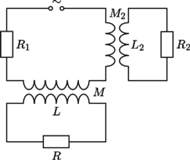
Jak wiadomo, w Europie częstotliwość sieciowa wynosi 50 Hz, a w USA - 60 Hz. Aby zrozumieć powód, dla którego niekorzystny byłby wybór częstotliwości znacznie większej lub znacznie mniejszej, rozważmy następujący model. Odbiornik energii (opornik 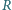 ) jest dołączony do źródła napięcia przemiennego przez transformator o indukcyjności uzwojenia wtórnego
) jest dołączony do źródła napięcia przemiennego przez transformator o indukcyjności uzwojenia wtórnego 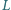 i współczynniku indukcji wzajemnej między uzwojeniami
i współczynniku indukcji wzajemnej między uzwojeniami 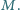 Ponadto w obwodzie występuje opornik
Ponadto w obwodzie występuje opornik 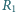 odpowiadający oporności przewodów i uzwojenia transformatora oraz drugi transformator opisany parametrami
odpowiadający oporności przewodów i uzwojenia transformatora oraz drugi transformator opisany parametrami 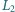 i
i 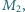 do którego dołączony jest opornik
do którego dołączony jest opornik 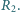 Ten drugi obwód symbolizuje prądy wirowe wzbudzane w przewodnikach, które przypadkiem znajdą się w pobliżu kabli doprowadzających energię do właściwego odbiornika.
Ten drugi obwód symbolizuje prądy wirowe wzbudzane w przewodnikach, które przypadkiem znajdą się w pobliżu kabli doprowadzających energię do właściwego odbiornika.
- a)
- Jaki warunek muszą spełniać wymienione parametry, aby stosunek strat energii (łącznej mocy traconej na opornikach
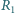 i
i 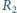 ) do mocy dostarczanej do opornika
) do mocy dostarczanej do opornika 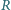 osiągał minimum dla pewnej częstotliwości?
osiągał minimum dla pewnej częstotliwości? - b)
- Jeśli powyższy warunek jest spełniony, to jakim wzorem dana jest optymalna częstotliwość?
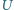 ze źródła zasilania, a do pozostałych dwóch dołączamy woltomierz o bardzo wielkim oporze własnym i mierzymy napięcie
ze źródła zasilania, a do pozostałych dwóch dołączamy woltomierz o bardzo wielkim oporze własnym i mierzymy napięcie 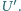 Istnieje sześć możliwych sposobów przyłączenia zasilania i woltomierza do "czarnej skrzynki", a zatem sześć możliwych wartości
Istnieje sześć możliwych sposobów przyłączenia zasilania i woltomierza do "czarnej skrzynki", a zatem sześć możliwych wartości 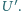 Zaprojektować taki możliwie najprostszy schemat "czarnej skrzynki", aby wśród nich znalazły się
Zaprojektować taki możliwie najprostszy schemat "czarnej skrzynki", aby wśród nich znalazły się 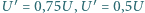 i
i 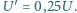
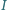 wypadkowego drgania powstałego w wyniku dodawania się dwóch fal elektromagnetycznych o takiej samej częstości i o natężeniach
wypadkowego drgania powstałego w wyniku dodawania się dwóch fal elektromagnetycznych o takiej samej częstości i o natężeniach 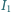 i
i 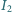 będzie równe sumie natężeń drgań składowych niezależnie od różnicy faz między nimi?
będzie równe sumie natężeń drgań składowych niezależnie od różnicy faz między nimi?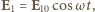 a drugiej
a drugiej 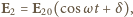 gdzie
gdzie 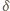 jest różnicą faz między drganiami. Drganie wypadkowe będzie dane wzorem
jest różnicą faz między drganiami. Drganie wypadkowe będzie dane wzorem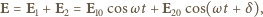
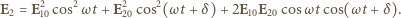
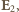 czyli
czyli
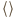 oznacza średnią względem czasu. Wyrażenie to będzie równe zero niezależnie od wartości przesunięcia fazowego
oznacza średnią względem czasu. Wyrażenie to będzie równe zero niezależnie od wartości przesunięcia fazowego 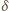 jeżeli iloczyn skalarny
jeżeli iloczyn skalarny 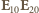 będzie równy zero, a to oznacza, że kierunki drgań muszą być względem siebie prostopadłe.
będzie równy zero, a to oznacza, że kierunki drgań muszą być względem siebie prostopadłe.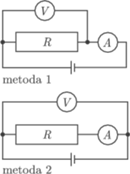
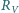 i amperomierz o oporze wewnętrznym
i amperomierz o oporze wewnętrznym 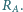 W celu wyznaczenia nieznanej wartości oporu
W celu wyznaczenia nieznanej wartości oporu 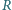 opornika możemy zestawić obwód pomiarowy na dwa różne sposoby (rysunek). Wykonując pomiary metodą 1, odczytaliśmy wartość prądu równą
opornika możemy zestawić obwód pomiarowy na dwa różne sposoby (rysunek). Wykonując pomiary metodą 1, odczytaliśmy wartość prądu równą 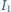 i napięcie równe
i napięcie równe 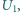 a pomiary metodą 2 dały wyniki
a pomiary metodą 2 dały wyniki 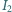 i
i 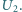 W jakich warunkach wartość obliczona na podstawie uproszczonego wzoru
W jakich warunkach wartość obliczona na podstawie uproszczonego wzoru 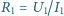 jest dokładniejszym przybliżeniem dokładnej wartości
jest dokładniejszym przybliżeniem dokładnej wartości 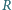 niż wartość
niż wartość 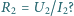 Zakładamy, że każdorazowo woltomierz poprawnie pokazuje różnicę potencjałów na jego zaciskach, a amperomierz poprawnie podaje wartość płynącego przezeń prądu.
Zakładamy, że każdorazowo woltomierz poprawnie pokazuje różnicę potencjałów na jego zaciskach, a amperomierz poprawnie podaje wartość płynącego przezeń prądu.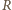 powinniśmy obliczać według wzorów:
powinniśmy obliczać według wzorów: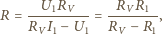
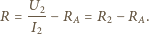
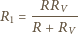
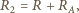
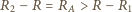
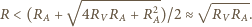
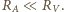
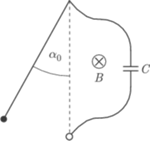
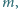 zawieszona na nieważkiej przewodzącej nici o długości
zawieszona na nieważkiej przewodzącej nici o długości 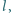 wykonuje małe drgania z amplitudą kątową
wykonuje małe drgania z amplitudą kątową 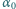 w płaszczyźnie pionowej, w jednorodnym polu magnetycznym o indukcji
w płaszczyźnie pionowej, w jednorodnym polu magnetycznym o indukcji 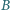 Linie pola magnetycznego są prostopadłe do płaszczyzny drgań wahadła. Gdy wahadło przechodzi przez położenie równowagi, podłączony zostaje do niego za pomocą cienkich, wiotkich przewodów kondensator o pojemności
Linie pola magnetycznego są prostopadłe do płaszczyzny drgań wahadła. Gdy wahadło przechodzi przez położenie równowagi, podłączony zostaje do niego za pomocą cienkich, wiotkich przewodów kondensator o pojemności 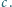 Czas kontaktu jest bardzo krótki i można przyjąć, że w tym czasie kondensator zostaje całkowicie naładowany. Znaleźć nową amplitudę kątową drgań wahadła.
Czas kontaktu jest bardzo krótki i można przyjąć, że w tym czasie kondensator zostaje całkowicie naładowany. Znaleźć nową amplitudę kątową drgań wahadła.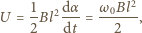
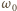 jest prędkością kątową wahadła w najniższym położeniu. Otrzymujemy ją z zasady zachowania energii, stosując przybliżenie małych kątów
jest prędkością kątową wahadła w najniższym położeniu. Otrzymujemy ją z zasady zachowania energii, stosując przybliżenie małych kątów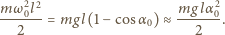
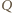 :
: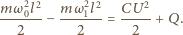
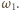 Czas kontaktu kulki z kondensatorem jest bardzo krótki, możemy więc przyjąć, że napięcie
Czas kontaktu kulki z kondensatorem jest bardzo krótki, możemy więc przyjąć, że napięcie 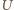 nie zmienia się podczas ładowania kondensatora. Źródło tego napięcia wykonuje zatem pracę
nie zmienia się podczas ładowania kondensatora. Źródło tego napięcia wykonuje zatem pracę 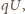 gdzie
gdzie 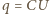 jest ładunkiem, do jakiego naładował się kondensator. Stąd
jest ładunkiem, do jakiego naładował się kondensator. Stąd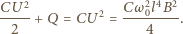
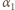 wahadła znajdujemy z równania
wahadła znajdujemy z równania 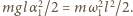 Uwzględniając (2), (3) i (4), dostajemy
Uwzględniając (2), (3) i (4), dostajemy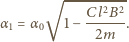
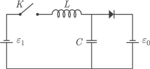
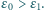 Jaki ładunek przepłynie przez źródło o sile elektromotorycznej
Jaki ładunek przepłynie przez źródło o sile elektromotorycznej 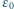 po zamknięciu klucza
po zamknięciu klucza 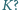 Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.
Zakładamy, że opór omowy cewki i opory wewnętrzne źródeł są równe zeru. Dioda jest idealna, czyli jej opór w kierunku przewodzenia wynosi zero, a w kierunku przeciwnym jest nieskończenie wielki. Przed zamknięciem klucza kondensator był nienaładowany.
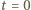 natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
natężenie prądu płynącego przez cewkę i ładunek na kondensatorze są równe zeru. Spełnione są równania
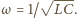 W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła
W obwodzie zachodzą drgania harmoniczne. Natężenie prądu płynącego przez cewkę osiąga maksymalną wartość, gdy znika jego pochodna po czasie, napięcie na kondensatorze równe jest wtedy sile elektromotorycznej źródła 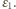 Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu
Kondensator ładuje się dalej kosztem energii pola magnetycznego w cewce. Gdy natężenie prądu 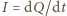 spada do zera, ładunek na kondensatorze osiąga maksymalną wartość
spada do zera, ładunek na kondensatorze osiąga maksymalną wartość 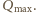 Zgodnie z zasadą zachowania energii mamy
Zgodnie z zasadą zachowania energii mamy 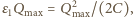 czyli maksymalne napięcie na kondensatorze wynosi
czyli maksymalne napięcie na kondensatorze wynosi 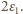
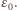 Gdy
Gdy 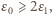 przez źródło o sile elektromotorycznej
przez źródło o sile elektromotorycznej 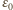 nie przepłynie żaden ładunek.
nie przepłynie żaden ładunek.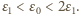 Gdy napięcie na kondensatorze osiąga wartość
Gdy napięcie na kondensatorze osiąga wartość 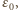 prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem
prąd płynie przez diodę kosztem energii pola magnetycznego w cewce zgodnie z równaniem 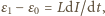 czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez
czyli natężenie prądu maleje liniowo w czasie. Do chwili, gdy jego wartość spadnie do zera, napięcie na kondensatorze nie zmienia się. Oznaczmy przez 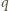 szukany ładunek przepływający przez źródło o sile elektromotorycznej
szukany ładunek przepływający przez źródło o sile elektromotorycznej 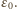 Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło
Od chwili zamknięcia klucza do chwili, kiedy przez diodę przestaje płynąć prąd, przez źródło 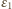 przepływa ładunek
przepływa ładunek 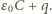 Bilans energetyczny dla całego procesu ma postać
Bilans energetyczny dla całego procesu ma postać 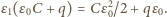 Stąd
Stąd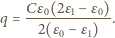
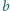 naładowana jest ze stałą gęstością objętościową
naładowana jest ze stałą gęstością objętościową 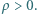 Wewnątrz kuli znajduje się uziemiona, metalowa sfera o promieniu
Wewnątrz kuli znajduje się uziemiona, metalowa sfera o promieniu  Znaleźć ładunek indukowany na tej sferze.
Znaleźć ładunek indukowany na tej sferze.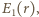 gdzie
gdzie  jest odległością od środka kuli. Dla
jest odległością od środka kuli. Dla 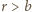 mamy zgodnie z prawem Gaussa
mamy zgodnie z prawem Gaussa 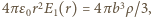 czyli pole
czyli pole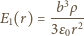
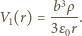
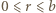 mamy
mamy 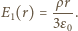 Aby otrzymać potencjał w tym obszarze, do potencjału
Aby otrzymać potencjał w tym obszarze, do potencjału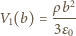
 od środka kuli do punktu na powierzchni kuli:
od środka kuli do punktu na powierzchni kuli: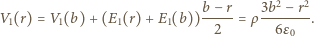
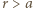 dane jest wzorem
dane jest wzorem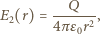
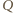 jest ładunkiem indukowanym na sferze. Potencjał w tym obszarze jest równy
jest ładunkiem indukowanym na sferze. Potencjał w tym obszarze jest równy 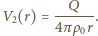 Wypadkowy potencjał uziemionej sfery to
Wypadkowy potencjał uziemionej sfery to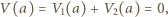
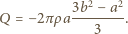
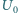 i po odłączeniu od źródła napięcia podłączono do niego opornik. W pewnym przedziale czasu na oporniku wydzieliła się w postaci ciepła energia
i po odłączeniu od źródła napięcia podłączono do niego opornik. W pewnym przedziale czasu na oporniku wydzieliła się w postaci ciepła energia 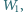 a w następnym takim samym przedziale czasu energia
a w następnym takim samym przedziale czasu energia 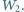 Znaleźć pojemność kondensatora.
Znaleźć pojemność kondensatora.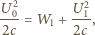
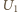 jest napięciem na kondensatorze po upływie czasu
jest napięciem na kondensatorze po upływie czasu 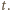 Gdy kondensator rozładowuje się przez opornik, natężenie prądu maleje wykładniczo w czasie
Gdy kondensator rozładowuje się przez opornik, natężenie prądu maleje wykładniczo w czasie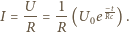
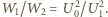 Szukana pojemność kondensatora wynosi
Szukana pojemność kondensatora wynosi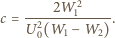
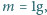 którą naładowano ładunkiem
którą naładowano ładunkiem 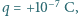 wystrzelono z dużej odległości z prędkością
wystrzelono z dużej odległości z prędkością 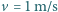 w kierunku metalowej sfery, naładowanej ładunkiem
w kierunku metalowej sfery, naładowanej ładunkiem 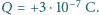 Przy jakim najmniejszym promieniu sfery kulka dotrze do jej powierzchni?
Przy jakim najmniejszym promieniu sfery kulka dotrze do jej powierzchni?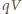 przeciw siłom pola elektrycznego (
przeciw siłom pola elektrycznego ( 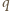 - ładunek kulki,
- ładunek kulki, 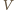 - przebyta przez nią różnica potencjałów). Energia kulki będzie malała zgodnie ze wzorem
- przebyta przez nią różnica potencjałów). Energia kulki będzie malała zgodnie ze wzorem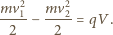
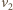 jest nieujemna. Dla granicznego przypadku mamy
jest nieujemna. Dla granicznego przypadku mamy 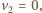 więc
więc 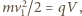 gdzie
gdzie 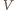 - potencjał sfery (przyjęliśmy, że potencjał odległego punktu wystrzelenia kulki wynosi zero). Korzystając z tego, że potencjał sfery wyraża się jako
- potencjał sfery (przyjęliśmy, że potencjał odległego punktu wystrzelenia kulki wynosi zero). Korzystając z tego, że potencjał sfery wyraża się jako 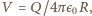 gdzie
gdzie 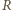 to promień sfery, otrzymamy
to promień sfery, otrzymamy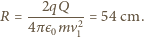

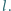 Drugim końcem dotyka pierścienia. Siła tarcia w ruchomym kontakcie wynosi
Drugim końcem dotyka pierścienia. Siła tarcia w ruchomym kontakcie wynosi 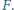 Jednorodne pole magnetyczne o indukcji
Jednorodne pole magnetyczne o indukcji 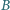 jest prostopadłe do powierzchni pierścienia. Siła elektromotoryczna ogniwa wynosi
jest prostopadłe do powierzchni pierścienia. Siła elektromotoryczna ogniwa wynosi 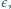 opór obwodu jest równy
opór obwodu jest równy 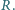 Znaleźć ustaloną prędkość pręta i natężenie prądu w obwodzie.
Znaleźć ustaloną prędkość pręta i natężenie prądu w obwodzie.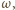 w wyniku zmiany strumienia pola magnetycznego
w wyniku zmiany strumienia pola magnetycznego 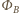 przez powierzchnię obwodu powstaje siła elektromotoryczna indukcji, której wartość wynosi
przez powierzchnię obwodu powstaje siła elektromotoryczna indukcji, której wartość wynosi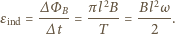
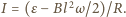 Warunek równowagi momentów sił działających na obracający się ze stałą prędkością kątową pręt ma postać
Warunek równowagi momentów sił działających na obracający się ze stałą prędkością kątową pręt ma postać 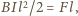 stąd
stąd 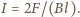 Z porównania wzorów na natężenie prądu otrzymujemy ustaloną prędkość kątową pręta:
Z porównania wzorów na natężenie prądu otrzymujemy ustaloną prędkość kątową pręta: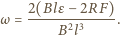
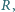 gdy nie znamy oporów wewnętrznych woltomierza i amperomierza?
gdy nie znamy oporów wewnętrznych woltomierza i amperomierza?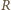 i amperomierz; następnie podłączamy woltomierz równolegle do amperomierza i notujemy wskazania obu przyrządów, tj. napięcie
i amperomierz; następnie podłączamy woltomierz równolegle do amperomierza i notujemy wskazania obu przyrządów, tj. napięcie 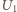 i prąd
i prąd 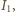 a następnie podłączamy woltomierz równolegle do oporu
a następnie podłączamy woltomierz równolegle do oporu 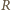 i rejestrujemy napięcie
i rejestrujemy napięcie 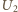 i prąd
i prąd 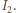 Pierwszy pomiar pozwala wyznaczyć opór wewnętrzny amperomierza,
Pierwszy pomiar pozwala wyznaczyć opór wewnętrzny amperomierza, 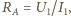 a drugi sumę oporu
a drugi sumę oporu 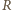 i
i 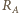 :
: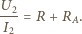
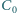 połączono cewką o indukcyjności
połączono cewką o indukcyjności 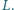 Jak należy zmniejszać pojemność kondensatora w zależności od czasu, aby prąd w obwodzie rósł wprost proporcjonalnie do czasu?
Jak należy zmniejszać pojemność kondensatora w zależności od czasu, aby prąd w obwodzie rósł wprost proporcjonalnie do czasu?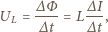
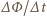 - szybkość zmian strumienia pola magnetycznego przez cewkę,
- szybkość zmian strumienia pola magnetycznego przez cewkę, 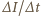 - szybkość zmian natężenia prądu w cewce (
- szybkość zmian natężenia prądu w cewce ( 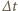 małe). Ponieważ prąd w cewce ma rosnąć proporcjonalnie do czasu, napięcie
małe). Ponieważ prąd w cewce ma rosnąć proporcjonalnie do czasu, napięcie 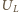 nie zmienia się w czasie i w dowolnym momencie wynosi
nie zmienia się w czasie i w dowolnym momencie wynosi 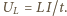 Napięcie na kondensatorze, które jest równe napięciu na cewce, także pozostaje stałe i wynosi
Napięcie na kondensatorze, które jest równe napięciu na cewce, także pozostaje stałe i wynosi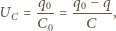
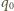 - początkowy ładunek na kondensatorze,
- początkowy ładunek na kondensatorze, 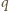 - ładunek, który wypłynął z kondensatora w czasie
- ładunek, który wypłynął z kondensatora w czasie 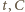 -pojemność kondensatora w momencie
-pojemność kondensatora w momencie 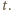 Z równości
Z równości 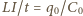 dostajemy
dostajemy 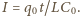 Ładunek, który wypłynął z kondensatora w czasie
Ładunek, który wypłynął z kondensatora w czasie 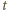 wynosi
wynosi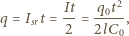
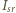 - średnia wartość natężenia prądu w czasie
- średnia wartość natężenia prądu w czasie 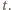 Z warunku stałości napięcia na kondensatorze znajdujemy szukaną zależność pojemności od czas
Z warunku stałości napięcia na kondensatorze znajdujemy szukaną zależność pojemności od czas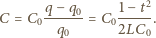
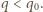
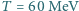 - taką wiązką dysponuje Cyklotron Instytutu Fizyki Jądrowej w Krakowie - poruszała się wzdłuż łuku okręgu o promieniu
- taką wiązką dysponuje Cyklotron Instytutu Fizyki Jądrowej w Krakowie - poruszała się wzdłuż łuku okręgu o promieniu 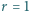 m? Jaka musiałaby być wartość indukcji
m? Jaka musiałaby być wartość indukcji 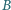 pola magnetycznego, żeby wywołać takie samo zakrzywienie toru tej wiązki? Masa protonu wynosi
pola magnetycznego, żeby wywołać takie samo zakrzywienie toru tej wiązki? Masa protonu wynosi 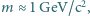 a prędkość światła c
a prędkość światła c 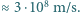
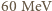 to mniej niż 1/15 masy spoczynkowej protonu, a więc do oszacowań możemy zastosować przybliżenie nierelatywistyczne. Oddziaływanie z polem prostopadłym do toru jest źródłem siły dośrodkowej. Mamy więc:
to mniej niż 1/15 masy spoczynkowej protonu, a więc do oszacowań możemy zastosować przybliżenie nierelatywistyczne. Oddziaływanie z polem prostopadłym do toru jest źródłem siły dośrodkowej. Mamy więc: 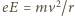 w przypadku pola elektrycznego i
w przypadku pola elektrycznego i 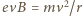 w przypadku pola magnetycznego, gdzie
w przypadku pola magnetycznego, gdzie  oznacza ładunek elementarny, a
oznacza ładunek elementarny, a  - prędkość protonów. Po skorzystaniu z faktu, że
- prędkość protonów. Po skorzystaniu z faktu, że 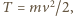 otrzymujemy:
otrzymujemy: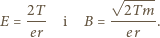
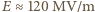 i
i 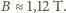 Pole elektryczne o otrzymanym natężeniu jest technicznie nieosiągalne, natomiast wartość
Pole elektryczne o otrzymanym natężeniu jest technicznie nieosiągalne, natomiast wartość 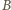 odpowiada w przybliżeniu indukcji tuż przy biegunie magnesu neodymowego używanego, na przykład, do pokazów.
odpowiada w przybliżeniu indukcji tuż przy biegunie magnesu neodymowego używanego, na przykład, do pokazów.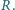 Protony wiązki poruszają się ze stałą prędkością
Protony wiązki poruszają się ze stałą prędkością 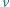 równolegle do osi wiązki. Jaka siła działa na proton poruszający się w odległości
równolegle do osi wiązki. Jaka siła działa na proton poruszający się w odległości 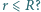 Przyjmujemy, że wewnątrz wiązki liczba protonów na jednostkę objętości jest stała i wynosi
Przyjmujemy, że wewnątrz wiązki liczba protonów na jednostkę objętości jest stała i wynosi 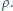
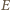 i
i 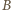 wzdłuż wiązki są równe zeru. Z symetrii układu wynika, że dla każdej wartości
wzdłuż wiązki są równe zeru. Z symetrii układu wynika, że dla każdej wartości  różne od zera mogą być tylko składowa pola
różne od zera mogą być tylko składowa pola 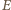 prostopadła do osi wiązki, skierowana od osi wiązki na zewnątrz i składowa pola
prostopadła do osi wiązki, skierowana od osi wiązki na zewnątrz i składowa pola 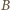 prostopadła do pola
prostopadła do pola 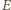 i do prędkości
i do prędkości 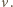 Wartości
Wartości 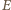 i
i 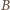 są przy tym jedynie funkcjami odległości
są przy tym jedynie funkcjami odległości  od osi wiązki. Na podstawie prawa Gaussa (obliczamy strumień
od osi wiązki. Na podstawie prawa Gaussa (obliczamy strumień 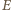 przez powierzchnię walca) mamy
przez powierzchnię walca) mamy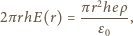
 oznacza ładunek protonu,
oznacza ładunek protonu, 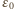 to przenikalność dielektryczna próżni, a
to przenikalność dielektryczna próżni, a 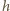 - "grubość plasterka" wiązki. Prawo Ampère'a (obliczamy krążenie wzdłuż okręgu o środku w centrum wiązki) prowadzi natomiast do równania
- "grubość plasterka" wiązki. Prawo Ampère'a (obliczamy krążenie wzdłuż okręgu o środku w centrum wiązki) prowadzi natomiast do równania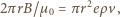
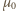 jest przenikalnością magnetyczną próżni. Podstawiając otrzymane w ten sposób wartości
jest przenikalnością magnetyczną próżni. Podstawiając otrzymane w ten sposób wartości 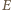 i
i 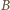 do wzoru na siłę Lorentza, otrzymujemy, że na proton wiązki działa siła
do wzoru na siłę Lorentza, otrzymujemy, że na proton wiązki działa siła 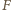 prostopadła do osi wiązki i skierowana na zewnątrz wiązki:
prostopadła do osi wiązki i skierowana na zewnątrz wiązki: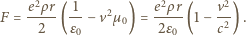

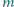 i stałej dielektrycznej
i stałej dielektrycznej 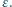 Okładki kondensatora mają rozmiary
Okładki kondensatora mają rozmiary 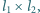 odległość między nimi wynosi
odległość między nimi wynosi 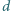 (
( 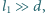
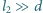 ). Między okładkami utrzymywane jest stałe napięcie
). Między okładkami utrzymywane jest stałe napięcie 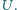 Płytkę wysunięto z obszaru kondensatora wzdłuż boku o długości
Płytkę wysunięto z obszaru kondensatora wzdłuż boku o długości 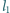 na odległość
na odległość 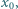 a następnie puszczono swobodnie. Zaniedbując tarcie, znaleźć zależność przemieszczenia i prędkości płytki od czasu.
a następnie puszczono swobodnie. Zaniedbując tarcie, znaleźć zależność przemieszczenia i prędkości płytki od czasu.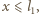 pojemność kondensatora wynosi
pojemność kondensatora wynosi ![c(x) = є0l2[x + є(l1− x)]/d,](/math/temat/fizyka/e_i_m/zadania/2016/05/01/zf-k44-619/2x-2e05e6822c69487536beed78f814b0b27b4b8119-im-66,57,43-FF,FF,FF.gif) energia
energia 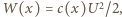 ładunek na okładkach
ładunek na okładkach 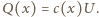 Oznaczając przez
Oznaczając przez 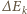 zmianę energii kinetycznej kondensatora, gdy położenie płytki zmienia się o
zmianę energii kinetycznej kondensatora, gdy położenie płytki zmienia się o 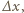 możemy napisać bilans energii:
możemy napisać bilans energii: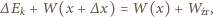
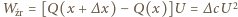 jest pracą źródła. Stąd
jest pracą źródła. Stąd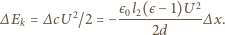


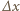 jest małe, możemy przyjąć, że siła
jest małe, możemy przyjąć, że siła 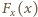 działająca na dielektryk wzdłuż osi
działająca na dielektryk wzdłuż osi 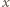 nie zmienia się, zatem
nie zmienia się, zatem 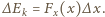 Dla dodatnich
Dla dodatnich 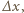 energia kinetyczna maleje, dielektryk jest więc wciągany do kondensatora siłą o stałej wartości
energia kinetyczna maleje, dielektryk jest więc wciągany do kondensatora siłą o stałej wartości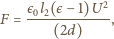
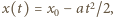 prędkość
prędkość 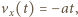 gdzie
gdzie 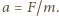 Dielektryk wykonuje więc drgania wokół położenia równowagi dla
Dielektryk wykonuje więc drgania wokół położenia równowagi dla 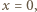 gdzie prędkość osiąga maksymalną wartość
gdzie prędkość osiąga maksymalną wartość 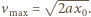 Okres drgań wynosi
Okres drgań wynosi 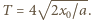 Zależność położenia i prędkości dielektryka od czasu przedstawiona jest na wykresach (rysunki 1 i 2), wykres położenia składa się z fragmentów parabol.
Zależność położenia i prędkości dielektryka od czasu przedstawiona jest na wykresach (rysunki 1 i 2), wykres położenia składa się z fragmentów parabol.
 wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie:
wartość wektora indukcji pola magnetycznego rośnie liniowo w czasie: 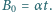 Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu
Linie pola magnetycznego są równoległe do osi walca. Jak musi zmieniać się w czasie wartość jednorodnego pola magnetycznego wewnątrz tej powierzchni, aby elektron poruszał się po okręgu o promieniu 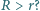 W chwili
W chwili 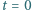 elektron spoczywa.
elektron spoczywa.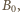 ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu
ponieważ wewnątrz powierzchni walcowej nie płynie żaden prąd. Jeżeli elektron porusza się po okręgu o promieniu 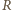 i ma w danej chwili prędkość
i ma w danej chwili prędkość 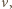 to działająca na niego siła dośrodkowa jest siłą Lorentza:
to działająca na niego siła dośrodkowa jest siłą Lorentza: 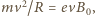 zatem jego prędkość
zatem jego prędkość 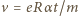 rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej
rośnie liniowo w czasie. Prędkość tę uzyskuje elektron dzięki sile elektrycznej 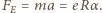 Wektor natężenia pola elektrycznego o długości
Wektor natężenia pola elektrycznego o długości 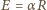 jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu
jest styczny do okręgu. Z prawa Maxwella wiemy, że krążenie pola elektrycznego wzdłuż okręgu o promieniu 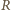 ma wartość bezwzględną
ma wartość bezwzględną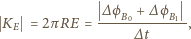
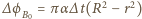 jest zmianą w czasie
jest zmianą w czasie 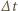 strumienia pola
strumienia pola 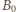 przez powierzchnię objętą okręgiem,
przez powierzchnię objętą okręgiem, 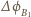 jest zmianą strumienia szukanego pola
jest zmianą strumienia szukanego pola 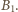 Ponieważ
Ponieważ 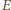 nie zależy od czasu,
nie zależy od czasu, 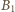 musi być liniową funkcją czasu:
musi być liniową funkcją czasu: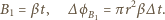
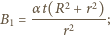
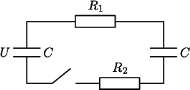
 drugi nie był naładowany. Pojemności kondensatorów są jednakowe i równe
drugi nie był naładowany. Pojemności kondensatorów są jednakowe i równe 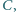 wartości oporów wynoszą
wartości oporów wynoszą 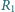 i
i 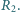
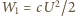 , a jego ładunek jest równy
, a jego ładunek jest równy 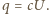 Po zamknięciu klucza napięcie na równolegle połączonych kondensatorach ma wartość
Po zamknięciu klucza napięcie na równolegle połączonych kondensatorach ma wartość 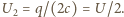 Energia układu kondensatorów wynosi
Energia układu kondensatorów wynosi 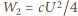 i jest mniejsza od początkowej o wielkość
i jest mniejsza od początkowej o wielkość 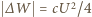 , równą całkowitemu wydzielonemu ciepłu
, równą całkowitemu wydzielonemu ciepłu 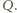 Natężenie prądu płynącego przez oba oporniki podczas przeładowywania kondensatorów jest w każdej chwili jednakowe, zatem ciepło wydzielone na oporze
Natężenie prądu płynącego przez oba oporniki podczas przeładowywania kondensatorów jest w każdej chwili jednakowe, zatem ciepło wydzielone na oporze 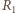 dane jest wzorem
dane jest wzorem 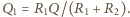 Ostatecznie
Ostatecznie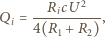
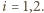
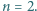 Gdy do uzwojenia pierwotnego przyłożono napięcie przemienne o amplitudzie
Gdy do uzwojenia pierwotnego przyłożono napięcie przemienne o amplitudzie 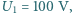 amplituda napięcia na otwartym uzwojeniu wtórnym wynosiła
amplituda napięcia na otwartym uzwojeniu wtórnym wynosiła 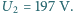 Jaka będzie amplituda napięcia na otwartym uzwojeniu wtórnym, gdy rdzeń transformatora zastąpimy rdzeniem o tych samych wymiarach, ale wykonanym z materiału o przenikalności magnetycznej
Jaka będzie amplituda napięcia na otwartym uzwojeniu wtórnym, gdy rdzeń transformatora zastąpimy rdzeniem o tych samych wymiarach, ale wykonanym z materiału o przenikalności magnetycznej 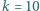 razy mniejszej niż w pierwszym przypadku? Rozpraszanie strumienia magnetycznego oraz straty w rdzeniu możemy zaniedbać.
razy mniejszej niż w pierwszym przypadku? Rozpraszanie strumienia magnetycznego oraz straty w rdzeniu możemy zaniedbać.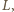 w drugim przez
w drugim przez 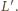 Współczynnik samoindukcji cewki jest proporcjonalny do przenikalności magnetycznej rdzenia, stąd
Współczynnik samoindukcji cewki jest proporcjonalny do przenikalności magnetycznej rdzenia, stąd 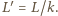 Uzwojenie możemy traktować jako połączenie szeregowe oporu czynnego
Uzwojenie możemy traktować jako połączenie szeregowe oporu czynnego 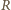 oraz indukcyjnego
oraz indukcyjnego 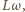 gdzie
gdzie 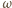 jest częstością napięcia zasilającego. Amplituda napięcia na oporze indukcyjnym wynosi
jest częstością napięcia zasilającego. Amplituda napięcia na oporze indukcyjnym wynosi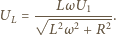
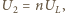 stąd
stąd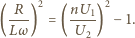
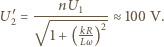
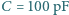 wypełniono roztworem soli kuchennej o oporze właściwym
wypełniono roztworem soli kuchennej o oporze właściwym 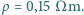 Ile wynosi opór elektryczny
Ile wynosi opór elektryczny 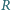 między elektrodami tak otrzymanego opornika? Przenikalność elektryczna próżni to
między elektrodami tak otrzymanego opornika? Przenikalność elektryczna próżni to 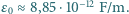
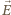 w każdym punkcie powierzchni każdej z elektrod jest do tej powierzchni prostopadły, a jego wartość jest proporcjonalna do napięcia
w każdym punkcie powierzchni każdej z elektrod jest do tej powierzchni prostopadły, a jego wartość jest proporcjonalna do napięcia 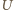 między elektrodami. Powierzchniowa gęstość ładunku w każdym punkcie elektrody kondensatora jest równa
między elektrodami. Powierzchniowa gęstość ładunku w każdym punkcie elektrody kondensatora jest równa 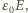 gdyż przenikalność elektryczna powietrza jest praktycznie równa przenikalności próżni. Normalna składowa gęstości prądu jest także proporcjonalna do wartości pola
gdyż przenikalność elektryczna powietrza jest praktycznie równa przenikalności próżni. Normalna składowa gęstości prądu jest także proporcjonalna do wartości pola 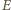 i jest równa
i jest równa 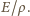 W związku z tym, przy tym samym napięciu
W związku z tym, przy tym samym napięciu 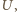 całkowity ładunek zgromadzony na powierzchni elektrod
całkowity ładunek zgromadzony na powierzchni elektrod 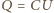 jest proporcjonalny do całkowitego prądu
jest proporcjonalny do całkowitego prądu 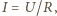 który popłynie po wypełnieniu kondensatora roztworem soli. Otrzymujemy więc:
który popłynie po wypełnieniu kondensatora roztworem soli. Otrzymujemy więc: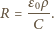
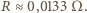
 może obracać się wokół pionowej osi, pokrywającej się z jego średnicą. W środku pierścienia umieszczono małą igiełkę magnetyczną, która może swobodnie obracać się wokół tej samej osi. Gdy pierścień jest nieruchomy, igiełka ustawia się wzdłuż składowej poziomej pola magnetycznego Ziemi
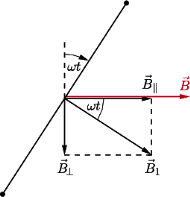
może obracać się wokół pionowej osi, pokrywającej się z jego średnicą. W środku pierścienia umieszczono małą igiełkę magnetyczną, która może swobodnie obracać się wokół tej samej osi. Gdy pierścień jest nieruchomy, igiełka ustawia się wzdłuż składowej poziomej pola magnetycznego Ziemi 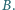 Pierścień wprowadzono w bardzo szybki ruch obrotowy ze stałą prędkością kątową
Pierścień wprowadzono w bardzo szybki ruch obrotowy ze stałą prędkością kątową 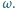 O jaki kąt odchyliła się igiełka od swego początkowego ustawienia? Opór pierścienia wynosi
O jaki kąt odchyliła się igiełka od swego początkowego ustawienia? Opór pierścienia wynosi 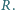
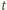 wynosi
wynosi 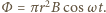 W pierścieniu powstaje prąd indukcyjny o natężeniu
W pierścieniu powstaje prąd indukcyjny o natężeniu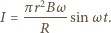
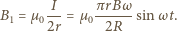
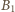 na składowe - równoległą i prostopadłą do wektora
na składowe - równoległą i prostopadłą do wektora 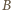 (
(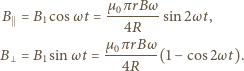
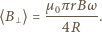
 (
(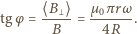

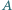 i
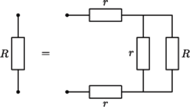
i 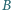 w obwodzie przedstawionym na rysunku. Opór każdej krawędzi między węzłami wynosi
w obwodzie przedstawionym na rysunku. Opór każdej krawędzi między węzłami wynosi 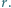 Sieć jest nieskończona w obie strony.
Sieć jest nieskończona w obie strony.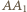 i
i 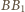 :
:
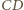 i
i 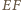 są jednakowe i równe
są jednakowe i równe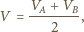
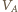 i
i 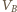 są potencjałami punktów
są potencjałami punktów 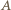 i
i 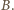 Zatem krawędzie między tymi węzłami można usunąć. Równoważny obwód składa się z dwóch nieskończonych obwodów połączonych równolegle i równoległego do nich opornika
Zatem krawędzie między tymi węzłami można usunąć. Równoważny obwód składa się z dwóch nieskończonych obwodów połączonych równolegle i równoległego do nich opornika  Opór
Opór 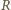 każdego z nieskończonych obwodów nie zmieni się, gdy dodamy do niego jeden z powtarzających się elementów. Wynika stąd równanie:
każdego z nieskończonych obwodów nie zmieni się, gdy dodamy do niego jeden z powtarzających się elementów. Wynika stąd równanie: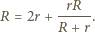
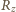 całego obwodu otrzymujemy z równania:
całego obwodu otrzymujemy z równania: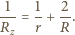
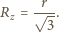

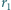 i
i 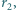 połączone przewodzącym drutem, znajdują się w dużej odległości od siebie. Kula o promieniu
połączone przewodzącym drutem, znajdują się w dużej odległości od siebie. Kula o promieniu 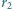 otoczona jest uziemioną sferą przewodzącą z małym otworkiem. Odległość sfery od kuli wynosi
otoczona jest uziemioną sferą przewodzącą z małym otworkiem. Odległość sfery od kuli wynosi 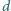 i jest dużo mniejsza od promienia kuli. Kule naładowano ładunkiem
i jest dużo mniejsza od promienia kuli. Kule naładowano ładunkiem 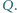 Wyznacz rozmieszczenie ładunku na kulach.
Wyznacz rozmieszczenie ładunku na kulach.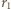 i
i 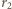 odpowiednio przez
odpowiednio przez 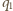 i
i 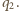 Zachodzi związek
Zachodzi związek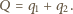
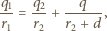
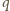 jest ładunkiem indukowanym na uziemionej sferze. Potencjał sfery jest równy zeru:
jest ładunkiem indukowanym na uziemionej sferze. Potencjał sfery jest równy zeru: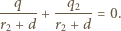
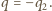 Podstawiając to do (2) i uwzględniając warunek
Podstawiając to do (2) i uwzględniając warunek 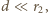 otrzymujemy związek:
otrzymujemy związek: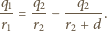
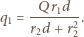
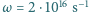 i amplitudzie modulowanej z częstością
i amplitudzie modulowanej z częstością 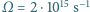 można zapisać jako
można zapisać jako
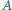 to stała). Znaleźć maksymalną energię elektronów "wybijanych" przez taką falę z atomów gazowego wodoru, dla którego energia jonizacji wynosi
to stała). Znaleźć maksymalną energię elektronów "wybijanych" przez taką falę z atomów gazowego wodoru, dla którego energia jonizacji wynosi 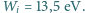
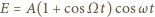
![1- 1- A cosωt+ 2 A cos[(ω− Ω)t]+ 2A cos[(ω+ Ω)t].](/math/temat/fizyka/e_i_m/zadania/2015/04/26/zf-880/2x-21d6d3717c73c4f923052865abde17ab5d19859f-dm-66,57,43-FF,FF,FF.gif)
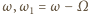 i
i 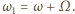 Energie fotonów odpowiadające każdej z tych fal wynoszą odpowiednio:
Energie fotonów odpowiadające każdej z tych fal wynoszą odpowiednio: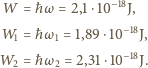
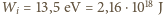 jest większa od energii
jest większa od energii 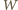 i energii
i energii 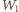 to fale o częstościach
to fale o częstościach 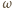 i
i 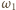 nie mogą spowodować jonizacji atomu wodoru, natomiast może ją spowodować fala o częstości
nie mogą spowodować jonizacji atomu wodoru, natomiast może ją spowodować fala o częstości 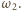 Maksymalna energia "wybitych" przez odpowiadające jej fotony elektronów będzie równa
Maksymalna energia "wybitych" przez odpowiadające jej fotony elektronów będzie równa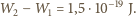
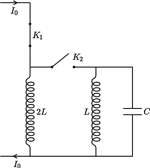
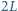 płynie prąd stały o natężeniu
płynie prąd stały o natężeniu 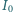 z zewnętrznego źródła. Po zamknięciu klucza
z zewnętrznego źródła. Po zamknięciu klucza 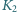 do cewki podłączamy równolegle cewkę o współczynniku samoindukcji
do cewki podłączamy równolegle cewkę o współczynniku samoindukcji 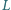 oraz kondensator o pojemności
oraz kondensator o pojemności 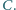 Następnie otwieramy klucz
Następnie otwieramy klucz 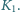 Znaleźć maksymalne napięcie na kondensatorze i maksymalne natężenie prądu płynącego w cewce o współczynniku samoindukcji
Znaleźć maksymalne napięcie na kondensatorze i maksymalne natężenie prądu płynącego w cewce o współczynniku samoindukcji 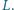 Elementy obwodu uważamy za idealne.
Elementy obwodu uważamy za idealne.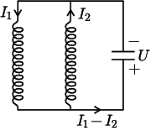
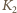 kondensator nie ładuje się, bo napięcie między końcami cewki o współczynniku samoindukcji
kondensator nie ładuje się, bo napięcie między końcami cewki o współczynniku samoindukcji 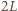 wynosi 0, a przez cewkę o współczynniku samoindukcji
wynosi 0, a przez cewkę o współczynniku samoindukcji 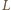 nie płynie prąd, gdyż zmiana natężenia prądu indukowałaby siłę elektromotoryczną na bezoporowej cewce. Po otwarciu obwodu zewnętrznego, oznaczając natężenia prądów jak na rysunku, mamy dla lewego oczka:
nie płynie prąd, gdyż zmiana natężenia prądu indukowałaby siłę elektromotoryczną na bezoporowej cewce. Po otwarciu obwodu zewnętrznego, oznaczając natężenia prądów jak na rysunku, mamy dla lewego oczka: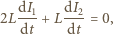
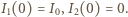 Stąd
Stąd 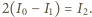 Ponieważ elementy obwodu uważamy za idealne, w obwodzie nie ma strat energii:
Ponieważ elementy obwodu uważamy za idealne, w obwodzie nie ma strat energii: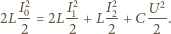
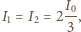 kondensator nie ładuje się ani nie rozładowuje i napięcie na nim jest maksymalne. Stąd
kondensator nie ładuje się ani nie rozładowuje i napięcie na nim jest maksymalne. Stąd 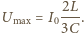 Natężenia prądów w cewkach są maksymalne, gdy ich pochodne, a tym samym siły elektromotoryczne samoindukcji są równe zeru. W tym momencie znika również napięcie na kondensatorze połączonym równolegle z cewkami i cała energia skupiona jest w cewkach:
Natężenia prądów w cewkach są maksymalne, gdy ich pochodne, a tym samym siły elektromotoryczne samoindukcji są równe zeru. W tym momencie znika również napięcie na kondensatorze połączonym równolegle z cewkami i cała energia skupiona jest w cewkach: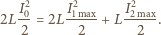
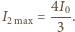

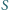 ustawiono równolegle. Pierwsza naładowana jest ładunkiem
ustawiono równolegle. Pierwsza naładowana jest ładunkiem 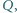 druga i trzecia połączone są drutem przewodzącym. Rozmiary liniowe płytek są dużo większe od odległości między nimi. Jaka siła działa na środkową płytkę?
druga i trzecia połączone są drutem przewodzącym. Rozmiary liniowe płytek są dużo większe od odległości między nimi. Jaka siła działa na środkową płytkę?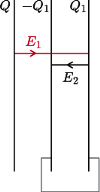
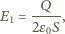
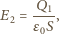
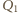 oznacza ładunek na trzeciej płytce równy co do wartości i o przeciwnym znaku niż ładunek na płytce drugiej. Wektory
oznacza ładunek na trzeciej płytce równy co do wartości i o przeciwnym znaku niż ładunek na płytce drugiej. Wektory 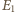 i
i 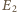 w obszarze między płytkami mają przeciwne zwroty i jednakowe wartości. Stąd
w obszarze między płytkami mają przeciwne zwroty i jednakowe wartości. Stąd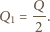
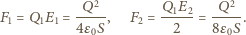
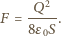
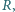 złożonej z dwóch półsfer, równomiernie rozłożony jest ładunek
złożonej z dwóch półsfer, równomiernie rozłożony jest ładunek 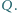 Jaką siłą trzeba działać na każdą półsferę, aby nie rozsuwały się one pod wpływem oddziaływania ładunków?
Jaką siłą trzeba działać na każdą półsferę, aby nie rozsuwały się one pod wpływem oddziaływania ładunków?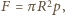 gdzie
gdzie 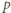 jest ciśnieniem wywieranym od wewnątrz na powierzchnię sfery, wywołanym oddziaływaniem ładunków. Aby wyznaczyć
jest ciśnieniem wywieranym od wewnątrz na powierzchnię sfery, wywołanym oddziaływaniem ładunków. Aby wyznaczyć 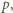 należy obliczyć pracę, jaką trzeba wykonać, zmniejszając promień sfery o małą wielkość
należy obliczyć pracę, jaką trzeba wykonać, zmniejszając promień sfery o małą wielkość 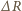 :
:![4-πp[R3-−-(R-−∆-R)3] 2 ∆W = p ∆ V = 3 ≈4 πR p ∆R.](/math/temat/fizyka/e_i_m/zadania/2014/12/28/zf-k44-591/5x-ea2d00b6e7ba9a495f7e052ea4a8cda665e28e15-dm-66,57,43-FF,FF,FF.gif)
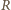 naładowanej ładunkiem
naładowanej ładunkiem 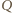 wynosi
wynosi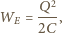
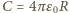 jest pojemnością sfery. Stąd
jest pojemnością sfery. Stąd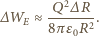
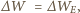 więc mamy
więc mamy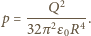
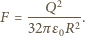
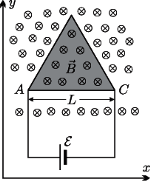
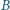 umieszczono cienką metalową płytkę, mającą kształt trójkąta równobocznego o boku
umieszczono cienką metalową płytkę, mającą kształt trójkąta równobocznego o boku 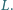 Grubość płytki wynosi
Grubość płytki wynosi 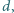 jej gęstość jest równa
jej gęstość jest równa 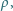 a jej powierzchnia jest prostopadła do kierunku pola magnetycznego. Do wierzchołków
a jej powierzchnia jest prostopadła do kierunku pola magnetycznego. Do wierzchołków 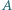 i
i 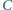 trójkąta dołączono źródło napięcia o sile elektromotorycznej
trójkąta dołączono źródło napięcia o sile elektromotorycznej 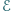 i oporności wewnętrznej
i oporności wewnętrznej 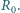 Znaleźć przyspieszenie płytki. Zaniedbać masę, oporność i sprężystość łączących przewodów oraz oporność płytki.
Znaleźć przyspieszenie płytki. Zaniedbać masę, oporność i sprężystość łączących przewodów oraz oporność płytki.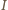 płynącego wzdłuż krzywej
płynącego wzdłuż krzywej 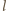 siła elektrodynamiczna działająca na element prądu
siła elektrodynamiczna działająca na element prądu 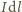 jest dana iloczynem wektorowym
jest dana iloczynem wektorowym 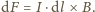 Ze względu na kształt rozważanego obwodu elektrycznego sumy składowych elementów prądu o zwrocie
Ze względu na kształt rozważanego obwodu elektrycznego sumy składowych elementów prądu o zwrocie 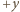 i
i 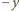 muszą mieć taką samą wartość, a w konsekwencji składowa
muszą mieć taką samą wartość, a w konsekwencji składowa  wypadkowej siły elektrodynamicznej wyniesie zero. Natomiast suma wszystkich składowych
wypadkowej siły elektrodynamicznej wyniesie zero. Natomiast suma wszystkich składowych 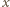 elementów prądu musi być skierowana od
elementów prądu musi być skierowana od 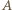 do
do 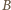 i musi być równa całkowitemu prądowi, przepływającemu przez płytkę, a długość składowej
i musi być równa całkowitemu prądowi, przepływającemu przez płytkę, a długość składowej  dowolnej drogi przepływu prądu musi być równa
dowolnej drogi przepływu prądu musi być równa 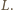 Stąd siła działająca na płytkę to
Stąd siła działająca na płytkę to 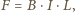 gdzie prąd
gdzie prąd 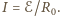 Masa płytki wynosi
Masa płytki wynosi 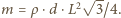 Z II zasady dynamiki dostajemy
Z II zasady dynamiki dostajemy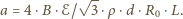
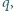 okazało się, że cząstka i kula przyciągają się z siłą
okazało się, że cząstka i kula przyciągają się z siłą 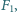 gdy naładowano kulę ładunkiem
gdy naładowano kulę ładunkiem 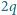 - cząstka i kula przyciągają się z siłą
- cząstka i kula przyciągają się z siłą 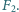 Jak duża będzie siła działająca pomiędzy cząstką i kulą, gdy ta ostatnia zostanie naładowana ładunkiem
Jak duża będzie siła działająca pomiędzy cząstką i kulą, gdy ta ostatnia zostanie naładowana ładunkiem 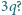
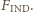 Jeżeli ładujemy kulę kolejno ładunkiem
Jeżeli ładujemy kulę kolejno ładunkiem 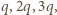 to pojawia się dodatkowa siła odpychania odpowiednio
to pojawia się dodatkowa siła odpychania odpowiednio 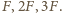 Znajdując wypadkową siłę działającą pomiędzy kulą i cząstką, w każdym z tych przypadków, dostajemy
Znajdując wypadkową siłę działającą pomiędzy kulą i cząstką, w każdym z tych przypadków, dostajemy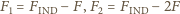
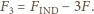
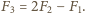 Zauważmy, że siła ta może być siłą przyciągania albo odpychania.
Zauważmy, że siła ta może być siłą przyciągania albo odpychania.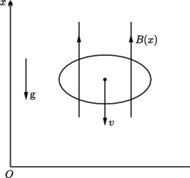
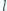 i oporze
i oporze 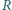 spada pod działaniem siły ciężkości w polu magnetycznym. Wartość wektora indukcji magnetycznej w kierunku pionowym zmienia się z wysokością zgodnie ze wzorem
spada pod działaniem siły ciężkości w polu magnetycznym. Wartość wektora indukcji magnetycznej w kierunku pionowym zmienia się z wysokością zgodnie ze wzorem
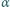 jest dodatnia. Znaleźć zależność siły hamującej ruch pierścienia od jego prędkości. Płaszczyzna pierścienia pozostaje prostopadła do linii pola magnetycznego.
jest dodatnia. Znaleźć zależność siły hamującej ruch pierścienia od jego prędkości. Płaszczyzna pierścienia pozostaje prostopadła do linii pola magnetycznego.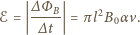
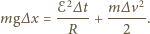
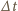 mamy:
mamy: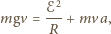
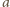 jest przyspieszeniem pierścienia. Równanie ruchu pierścienia ma postać:
jest przyspieszeniem pierścienia. Równanie ruchu pierścienia ma postać: 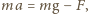 gdzie
gdzie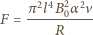
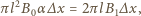
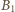 jest poziomą składową pola magnetycznego, prostopadłą do pierścienia. Siła elektrodynamiczna hamująca pierścień to
jest poziomą składową pola magnetycznego, prostopadłą do pierścienia. Siła elektrodynamiczna hamująca pierścień to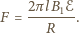
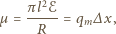
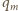 jest ładunkiem magnetycznym dipola. Siła hamująca wynosi
jest ładunkiem magnetycznym dipola. Siła hamująca wynosi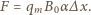

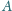 i
i
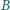 półnieskończonego
obwodu, jeżeli oporność każdego z jego elementów wynosi
półnieskończonego
obwodu, jeżeli oporność każdego z jego elementów wynosi
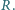
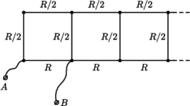
 wynika, że potencjały
punktów symetrycznych względem tej linii są jednakowe. Na tej podstawie
możemy rozpatrywany obwód zastąpić obwodem, który z kolei można
zwinąć do postaci z rysunku 2 i znaleźć oporność pomiędzy
punktami
wynika, że potencjały
punktów symetrycznych względem tej linii są jednakowe. Na tej podstawie
możemy rozpatrywany obwód zastąpić obwodem, który z kolei można
zwinąć do postaci z rysunku 2 i znaleźć oporność pomiędzy
punktami
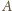 i
i
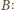
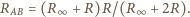
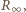 korzystamy z faktu, że oporność nieskończonego
obwodu jest taka sama z pierwszym jego ogniwem i bez niego. Stąd
korzystamy z faktu, że oporność nieskończonego
obwodu jest taka sama z pierwszym jego ogniwem i bez niego. Stąd
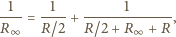
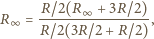
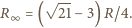
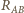 znajdujemy
znajdujemy