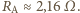Zadanie ZF-860
o zadaniu...
- Publikacja w Delcie: lipiec 2014
- Publikacja elektroniczna: 01-07-2014
Zmierzona przez satelity (tj. poza atmosferą) średnia wartość strumienia
energii promieniowania słonecznego (tzw. stała słoneczna) wynosi
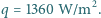 Jaki jest stosunek siły odpychającej Ziemię od Słońca
wynikającej z wywieranego przez to promieniowanie ciśnienia do siły
grawitacyjnego przyciągania Ziemi i Słońca?
Jaki jest stosunek siły odpychającej Ziemię od Słońca
wynikającej z wywieranego przez to promieniowanie ciśnienia do siły
grawitacyjnego przyciągania Ziemi i Słońca?
Dla uproszczenia przyjmujemy, że całe promieniowanie jest pochłaniane przez
Ziemię, przyspieszenie ziemskie wynosi
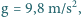 prędkość
światła
prędkość
światła
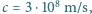 odległość Ziemia-Słońce to średnio
odległość Ziemia-Słońce to średnio
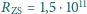 m, rok trwa w przybliżeniu
m, rok trwa w przybliżeniu
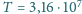 s, stała
grawitacji
s, stała
grawitacji
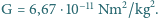
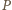 wynosi
wynosi
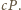 W związku z tym
pochłanianie przez Ziemię promieniowania słonecznego związane jest
z pochłanianiem strumienia pędu równego
W związku z tym
pochłanianie przez Ziemię promieniowania słonecznego związane jest
z pochłanianiem strumienia pędu równego
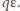 Związane
z pochłanianiem pędu promieniowania siła
Związane
z pochłanianiem pędu promieniowania siła
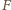 odpychająca od Słońca
Ziemię o promieniu
odpychająca od Słońca
Ziemię o promieniu
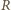 wynosi więc
wynosi więc
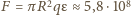 N. Siła
N. Siła
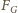 przyciągania Ziemi i Słońca wynosi:
przyciągania Ziemi i Słońca wynosi:
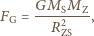
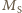 oznacza masę Słońca, a
oznacza masę Słońca, a
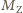 masę Ziemi. Przyspieszenie
Ziemi w ruchu dookoła Słońca wynosi
masę Ziemi. Przyspieszenie
Ziemi w ruchu dookoła Słońca wynosi
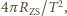 a masę Ziemi
możemy zastąpić wyrażeniem
a masę Ziemi
możemy zastąpić wyrażeniem
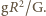 Po podstawieniu tych
wielkości otrzymujemy, że stosunek siły z jaką promieniowanie Słońca
odpycha Ziemię do siły przyciągania Ziemia-Słońce wynosi:
Po podstawieniu tych
wielkości otrzymujemy, że stosunek siły z jaką promieniowanie Słońca
odpycha Ziemię do siły przyciągania Ziemia-Słońce wynosi:
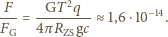
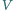 i ściankach doskonale odbijających
promieniowanie elektromagnetyczne wypełnione jest promieniowaniem
o całkowitej energii
i ściankach doskonale odbijających
promieniowanie elektromagnetyczne wypełnione jest promieniowaniem
o całkowitej energii
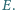 Jakie ciśnienie
Jakie ciśnienie
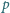 na ścianki naczynia
wywiera zawarte w nim promieniowanie elektromagnetyczne?
na ścianki naczynia
wywiera zawarte w nim promieniowanie elektromagnetyczne?
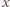 oznacza kierunek prostopadły do ścianki,
oznacza kierunek prostopadły do ścianki,
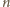 gęstość
fotonów, a
gęstość
fotonów, a
 średnią energię fotonu. Zderzając się sprężyście ze
ścianką foton o pędzie
średnią energię fotonu. Zderzając się sprężyście ze
ścianką foton o pędzie
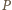 padający pod kątem
padający pod kątem
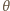 przekazuje jej
pęd
przekazuje jej
pęd
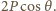 W jednostce czasu
W jednostce czasu
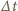 z każdego kierunku
tworzącego kąt
z każdego kierunku
tworzącego kąt
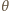 z normalną do każdego elementu ścianki
o powierzchni
z normalną do każdego elementu ścianki
o powierzchni
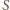 dolatuje więc
dolatuje więc
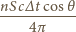
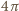 w mianowniku). Biorąc pod uwagę, że dla fotonu
w mianowniku). Biorąc pod uwagę, że dla fotonu
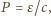 gdzie
gdzie
 jest prędkością światła, siła nacisku na ściankę
równa jest przekazowi pędu w jednostce czasu, a ciśnienie jest stosunkiem siły
nacisku do pola powierzchni, i sumując po wszystkich kątach padania,
otrzymujemy:
jest prędkością światła, siła nacisku na ściankę
równa jest przekazowi pędu w jednostce czasu, a ciśnienie jest stosunkiem siły
nacisku do pola powierzchni, i sumując po wszystkich kątach padania,
otrzymujemy:
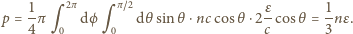
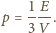
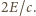
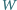 jest zamknięty i płynie prąd stały. Jaka ilość ciepła
wydzieli się w oporze
jest zamknięty i płynie prąd stały. Jaka ilość ciepła
wydzieli się w oporze
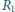 po otwarciu wyłącznika? Indukcyjność
cewki wynosi
po otwarciu wyłącznika? Indukcyjność
cewki wynosi
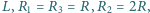 siła elektromotoryczna źródła
wynosi
siła elektromotoryczna źródła
wynosi
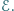 Oporność cewki oraz oporność wewnętrzna źródła
są zaniedbywalne.
Oporność cewki oraz oporność wewnętrzna źródła
są zaniedbywalne.
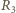 i cewkę, płynie
prąd
i cewkę, płynie
prąd
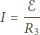
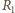 i
i
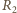 prąd nie płynie, bo spadek napięcia
na cewce jest równy zeru). Po otwarciu wyłącznika energia elektryczna
zgromadzona w cewce wydziela się w postaci ciepła
prąd nie płynie, bo spadek napięcia
na cewce jest równy zeru). Po otwarciu wyłącznika energia elektryczna
zgromadzona w cewce wydziela się w postaci ciepła
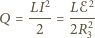
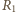 i
i
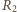 (przez opór
(przez opór
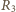 prąd nie płynie).
prąd nie płynie).
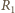 i
i
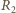 są połączone równolegle, więc spadki napięcia
na nich są równe
są połączone równolegle, więc spadki napięcia
na nich są równe
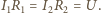 Ilość ciepła, jaka wydzieli się
w każdym z nich w ciągu krótkiego czasu
Ilość ciepła, jaka wydzieli się
w każdym z nich w ciągu krótkiego czasu
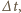 będzie równa
odpowiednio
będzie równa
odpowiednio
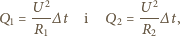
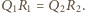 Równocześnie
Równocześnie
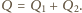 Ostatecznie
więc
Ostatecznie
więc
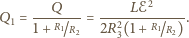
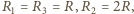 otrzymujemy
ostatecznie:
otrzymujemy
ostatecznie:
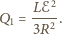
 do jakiego może naładować
się oddalona od innych ciał miedziana kulka oświetlona światłem
ultrafioletowym o długości fali
do jakiego może naładować
się oddalona od innych ciał miedziana kulka oświetlona światłem
ultrafioletowym o długości fali
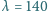 nm. Praca wyjścia dla miedzi
wynosi
nm. Praca wyjścia dla miedzi
wynosi
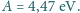
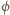 można wyrazić poprzez jej ładunek
można wyrazić poprzez jej ładunek
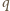 zależnością
zależnością
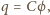 gdzie
gdzie
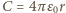 jest pojemnością kulki. Maksymalny
potencjał kulki
jest pojemnością kulki. Maksymalny
potencjał kulki
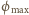 zależy od początkowej energii kinetycznej
elektronów. Ponieważ zmiana energii kinetycznej elektronów jest równa pracy
sił pola wytwarzanego przez kulkę, to przyjmując, że w nieskończoności
potencjał pola kulki i prędkość elektronu wynoszą zero i uwzględniając fakt,
że ładunek elektronu jest ujemny, można napisać:
zależy od początkowej energii kinetycznej
elektronów. Ponieważ zmiana energii kinetycznej elektronów jest równa pracy
sił pola wytwarzanego przez kulkę, to przyjmując, że w nieskończoności
potencjał pola kulki i prędkość elektronu wynoszą zero i uwzględniając fakt,
że ładunek elektronu jest ujemny, można napisać:
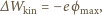
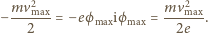
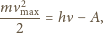
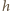 to stała Plancka,
to stała Plancka,
 – częstość światła. Podstawiając (2)
do (1), dostajemy
– częstość światła. Podstawiając (2)
do (1), dostajemy
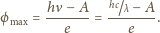
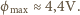
 i oporze właściwym
i oporze właściwym 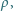 płynie prąd
płynie prąd 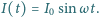 Znaleźć amplitudę napięcia na kondensatorze. Powierzchnia okładek kondensatora wynosi
Znaleźć amplitudę napięcia na kondensatorze. Powierzchnia okładek kondensatora wynosi 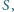 odległość między okładkami jest równa
odległość między okładkami jest równa 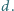

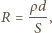 przez który płynie prąd o natężeniu
przez który płynie prąd o natężeniu 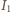 i kondensatora o pojemności
i kondensatora o pojemności 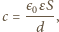 przez który płynie prąd o natężeniu
przez który płynie prąd o natężeniu 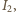 przy czym
przy czym 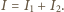 Napięcia na oporniku i kondensatorze są jednakowe:
Napięcia na oporniku i kondensatorze są jednakowe: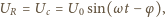
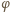 jest przesunięciem fazowym między napięciem i natężeniem prądu całkowitego
jest przesunięciem fazowym między napięciem i natężeniem prądu całkowitego 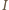 a
a 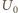 szukaną amplitudą napięcia. Ładunek na kondensatorze wynosi
szukaną amplitudą napięcia. Ładunek na kondensatorze wynosi 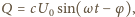 stąd
stąd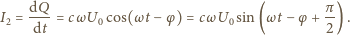
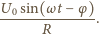
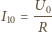 oraz
oraz 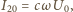 które tworzą ze sobą kąt
które tworzą ze sobą kąt  i obracają się wokół wspólnego punktu zaczepienia z prędkością kątową
i obracają się wokół wspólnego punktu zaczepienia z prędkością kątową 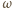 tak, że ich rzuty na wyróżnioną oś wynoszą
tak, że ich rzuty na wyróżnioną oś wynoszą 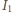 oraz
oraz 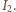 Wtedy wektor będący ich sumą wektorową ma długość
Wtedy wektor będący ich sumą wektorową ma długość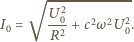
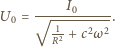
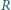 równomiernie rozłożony jest ładunek o gęstości powierzchniowej
równomiernie rozłożony jest ładunek o gęstości powierzchniowej
 Walec znajduje się w jednorodnym polu magnetycznym o indukcji
Walec znajduje się w jednorodnym polu magnetycznym o indukcji
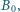 którego linie są równoległe do osi walca. Znaleźć prędkość
kątową walca po wyłączeniu zewnętrznego pola magnetycznego. Walec ma
jednorodną gęstość
którego linie są równoległe do osi walca. Znaleźć prędkość
kątową walca po wyłączeniu zewnętrznego pola magnetycznego. Walec ma
jednorodną gęstość
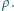
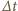 czas, w którym następuje wyłączenie zewnętrznego
pola magnetycznego. Zmiana strumienia tego pola przez powierzchnię przekroju
poprzecznego walca powoduje powstanie stycznego do powierzchni walca pola
elektrycznego, które działa na ładunek na powierzchni walca i wywołuje jego
obrót. Z kolei poruszający się ładunek powierzchniowy wytwarza wewnątrz
walca dodatkowe pole magnetyczne, które zgodnie z regułą przekory
rośnie w czasie i skierowane jest zgodnie z polem
czas, w którym następuje wyłączenie zewnętrznego
pola magnetycznego. Zmiana strumienia tego pola przez powierzchnię przekroju
poprzecznego walca powoduje powstanie stycznego do powierzchni walca pola
elektrycznego, które działa na ładunek na powierzchni walca i wywołuje jego
obrót. Z kolei poruszający się ładunek powierzchniowy wytwarza wewnątrz
walca dodatkowe pole magnetyczne, które zgodnie z regułą przekory
rośnie w czasie i skierowane jest zgodnie z polem
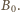 Oznaczmy
maksymalną wartość wektora tego pola przez
Oznaczmy
maksymalną wartość wektora tego pola przez
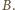 Zgodnie z prawem
Faradaya
Zgodnie z prawem
Faradaya
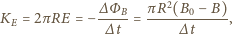
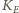 oznaczyliśmy krążenie pola elektrycznego
oznaczyliśmy krążenie pola elektrycznego
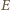 wzdłuż
okręgu o promieniu
wzdłuż
okręgu o promieniu
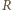 otaczającego przekrój poprzeczny walca, a przez
otaczającego przekrój poprzeczny walca, a przez
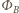 strumień pola magnetycznego przez powierzchnię tego przekroju.
Wartość indukowanego pola magnetycznego, gdy obracający się walec osiągnie
końcową prędkość kątową
strumień pola magnetycznego przez powierzchnię tego przekroju.
Wartość indukowanego pola magnetycznego, gdy obracający się walec osiągnie
końcową prędkość kątową
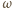 wynosi
wynosi
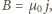 gdzie
gdzie
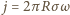 jest natężeniem prądu na jednostkę długości walca. Średni
moment siły zwiększający prędkość kątową walca w czasie
jest natężeniem prądu na jednostkę długości walca. Średni
moment siły zwiększający prędkość kątową walca w czasie
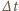 dany jest
wzorem
dany jest
wzorem
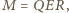 gdzie
gdzie
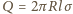 jest całkowitym ładunkiem
na powierzchni walca o długości
jest całkowitym ładunkiem
na powierzchni walca o długości
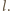 Równanie ruchu obrotowego walca
ma postać
Równanie ruchu obrotowego walca
ma postać
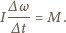
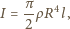
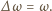 Wstawiając natężenie pola
Wstawiając natężenie pola
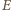 z prawa Faradaya
do równania ruchu obrotowego, otrzymujemy szukaną prędkość
kątową:
z prawa Faradaya
do równania ruchu obrotowego, otrzymujemy szukaną prędkość
kątową:

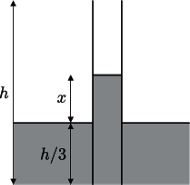
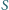 i wysokości
i wysokości
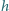 są skierowane pionowo i zanurzone w cieczy o stałej dielektrycznej
są skierowane pionowo i zanurzone w cieczy o stałej dielektrycznej
 do wysokości
do wysokości
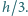 Oblicz ładunek, jakim naładowany jest
kondensator, jeżeli w stanie równowagi ciecz wypełnia całą przestrzeń między
okładkami. Gęstość cieczy wynosi
Oblicz ładunek, jakim naładowany jest
kondensator, jeżeli w stanie równowagi ciecz wypełnia całą przestrzeń między
okładkami. Gęstość cieczy wynosi
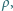 odległość między okładkami
jest mała w porównaniu z rozmiarami liniowymi okładek.
odległość między okładkami
jest mała w porównaniu z rozmiarami liniowymi okładek.
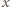 nad poziomem cieczy w naczyniu. Siła elektryczna
nad poziomem cieczy w naczyniu. Siła elektryczna
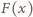 spowodowana niejednorodnością pola elektrycznego na brzegu
kondensatora, pracując na małym odcinku
spowodowana niejednorodnością pola elektrycznego na brzegu
kondensatora, pracując na małym odcinku
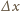 (dla którego można
przyjąć, że wartość siły nie zmienia się), powoduje zmniejszenie energii
elektrycznej kondensatora:
(dla którego można
przyjąć, że wartość siły nie zmienia się), powoduje zmniejszenie energii
elektrycznej kondensatora:
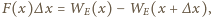 gdzie
gdzie
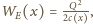 zaś
zaś
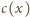 jest pojemnością zastępczą
dwóch kondensatorów połączonych równolegle – powietrznego
o wysokości
jest pojemnością zastępczą
dwóch kondensatorów połączonych równolegle – powietrznego
o wysokości
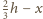 oraz wypełnionego dielektrykiem o wysokości
oraz wypełnionego dielektrykiem o wysokości
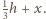 Wyrażenie na siłę elektryczną możemy obliczyć
bezpośrednio z wzoru
Wyrażenie na siłę elektryczną możemy obliczyć
bezpośrednio z wzoru
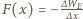 przy
przy
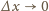 lub obliczyć
pochodną
lub obliczyć
pochodną
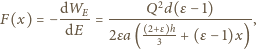
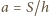 jest szerokością okładek kondensatora, zaś
jest szerokością okładek kondensatora, zaś
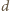 odległością między okładkami. Wartość siły grawitacji działającej na
ciecz wciągniętą do kondensatora wynosi
odległością między okładkami. Wartość siły grawitacji działającej na
ciecz wciągniętą do kondensatora wynosi
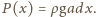 Z warunku
równowagi sił elektrycznej i grawitacyjnej dla
Z warunku
równowagi sił elektrycznej i grawitacyjnej dla
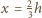 otrzymujemy
szukaną wartość ładunku
otrzymujemy
szukaną wartość ładunku
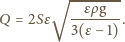
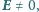 a indukcja
magnetyczna pola równa jest zeru. Jakie natężenie pola elektrycznego zmierzy
drugi obserwator, poruszający się względem pierwszego z prędkością
a indukcja
magnetyczna pola równa jest zeru. Jakie natężenie pola elektrycznego zmierzy
drugi obserwator, poruszający się względem pierwszego z prędkością
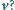
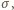 a wektor natężenia pola jest prostopadły do płaszczyzny.
a wektor natężenia pola jest prostopadły do płaszczyzny.
 równoległą do naładowanej
płaszczyzny stwierdzi, że powierzchniowa gęstość zgromadzonego na niej
ładunku wynosi
równoległą do naładowanej
płaszczyzny stwierdzi, że powierzchniowa gęstość zgromadzonego na niej
ładunku wynosi
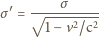
 oznacza prędkość światła), a więc mierzona przez niego
wartość składowej natężenia pola elektrycznego prostopadłej do płaszczyzny
to
oznacza prędkość światła), a więc mierzona przez niego
wartość składowej natężenia pola elektrycznego prostopadłej do płaszczyzny
to
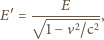
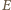 oznacza wartość mierzoną w układzie spoczynkowym
płaszczyzny.
oznacza wartość mierzoną w układzie spoczynkowym
płaszczyzny.
 ) zmierzy taką samą wartość składowej pola równoległej
do jego kierunku ruchu, jak obserwator spoczywający i
) zmierzy taką samą wartość składowej pola równoległej
do jego kierunku ruchu, jak obserwator spoczywający i
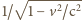 razy
większą wartość składowej prostopadłej.
razy
większą wartość składowej prostopadłej.

 wisi na elektrycznie izolowanej
nici. Znaleźć pracę, jaką należy wykonać, przybliżając z daleka
i bardzo wolno drugą naładowaną kulkę i umieszczając ją w miejscu, gdzie
przedtem znajdowała się kulka wisząca na nici. Pierwsza kulka odchyliła się
i podniosła na wysokość
wisi na elektrycznie izolowanej
nici. Znaleźć pracę, jaką należy wykonać, przybliżając z daleka
i bardzo wolno drugą naładowaną kulkę i umieszczając ją w miejscu, gdzie
przedtem znajdowała się kulka wisząca na nici. Pierwsza kulka odchyliła się
i podniosła na wysokość
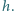 Przyspieszenie ziemskie
Przyspieszenie ziemskie
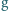 jest
dane.
jest
dane.
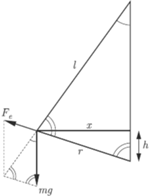
 powoduje wzrost energii potencjalnej ciężkości
zawieszonej kulki oraz energii potencjalnej oddziaływania elektrostatycznego
między kulkami
powoduje wzrost energii potencjalnej ciężkości
zawieszonej kulki oraz energii potencjalnej oddziaływania elektrostatycznego
między kulkami
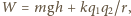 gdzie
gdzie
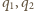 są ładunkami
kulek, a
są ładunkami
kulek, a
 końcową odległością między kulkami. Z podobieństwa
trójkątów przedstawionych na rysunku otrzymujemy
końcową odległością między kulkami. Z podobieństwa
trójkątów przedstawionych na rysunku otrzymujemy
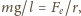 gdzie
gdzie
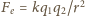 jest siłą elektrostatycznego oddziaływania między kulkami
w stanie równowagi. Zachodzi też związek
jest siłą elektrostatycznego oddziaływania między kulkami
w stanie równowagi. Zachodzi też związek
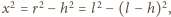 stąd
stąd
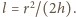 Energia oddziaływania elektrostatycznego między kulkami
wynosi
Energia oddziaływania elektrostatycznego między kulkami
wynosi
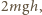 a szukana praca
a szukana praca
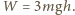
 znajduje się
w jednorodnym polu magnetycznym, którego indukcja magnetyczna jest
prostopadła do płaszczyzny zawierającej obręcz i zmienia się z czasem
znajduje się
w jednorodnym polu magnetycznym, którego indukcja magnetyczna jest
prostopadła do płaszczyzny zawierającej obręcz i zmienia się z czasem
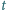 zgodnie ze wzorem
zgodnie ze wzorem
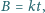 gdzie
gdzie
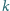 jest stałym
współczynnikiem proporcjonalności. Na skutek zmian pola magnetycznego
wytworzone zostaje pole elektryczne. Znaleźć natężenie pola elektrycznego
jest stałym
współczynnikiem proporcjonalności. Na skutek zmian pola magnetycznego
wytworzone zostaje pole elektryczne. Znaleźć natężenie pola elektrycznego
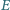 na obręczy.
na obręczy.
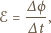
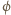 to strumień wektora indukcji magnetycznej. Z warunków
zadania mamy
to strumień wektora indukcji magnetycznej. Z warunków
zadania mamy
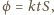 a więc
a więc
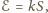 gdzie
gdzie
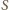 jest polem
powierzchni ograniczonej obręczą. Ze względu na symetrię zagadnienia
wartość pola elektrycznego w każdym punkcie obręczy jest taka sama.
Ponieważ wartość liczbowa siły elektromotorycznej indukcji jest z definicji
równa wykonanej przez zewnętrzne źródło energii pracy potrzebnej na
jednokrotny obieg obwodu przez jednostkowy ładunek elektryczny, więc
zachodzi związek
jest polem
powierzchni ograniczonej obręczą. Ze względu na symetrię zagadnienia
wartość pola elektrycznego w każdym punkcie obręczy jest taka sama.
Ponieważ wartość liczbowa siły elektromotorycznej indukcji jest z definicji
równa wykonanej przez zewnętrzne źródło energii pracy potrzebnej na
jednokrotny obieg obwodu przez jednostkowy ładunek elektryczny, więc
zachodzi związek
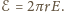 Stąd
Stąd
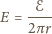
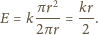

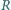 może
poruszać się bez tarcia pręt o masie
może
poruszać się bez tarcia pręt o masie
 Układ znajduje się
w jednorodnym polu magnetycznym o indukcji
Układ znajduje się
w jednorodnym polu magnetycznym o indukcji
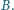 Linie pola
magnetycznego są prostopadłe do płaszczyzny szyn. Odległość między
szynami wynosi
Linie pola
magnetycznego są prostopadłe do płaszczyzny szyn. Odległość między
szynami wynosi
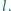 W chwili początkowej prętowi nadano prędkość
W chwili początkowej prętowi nadano prędkość
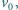 równoległą do szyn. Jaką drogę przebędzie pręt do momentu
zatrzymania? Jaki ładunek przepłynie w tym czasie przez opór
równoległą do szyn. Jaką drogę przebędzie pręt do momentu
zatrzymania? Jaki ładunek przepłynie w tym czasie przez opór
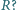 Opór
szyn i pręta zaniedbujemy.
Opór
szyn i pręta zaniedbujemy.
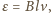 gdzie
gdzie
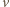 jest
chwilową prędkością pręta. Na pręt, w którym płynie prąd indukcyjny, działa
hamująca siła elektrodynamiczna o wartości
jest
chwilową prędkością pręta. Na pręt, w którym płynie prąd indukcyjny, działa
hamująca siła elektrodynamiczna o wartości
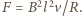 Zgodnie
z drugą zasadą dynamiki
Zgodnie
z drugą zasadą dynamiki
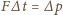 i możemy napisać:
i możemy napisać:
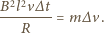
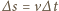 jest drogą przebytą w przedziale czasu
jest drogą przebytą w przedziale czasu
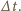 Po zsumowaniu otrzymujemy
Po zsumowaniu otrzymujemy
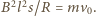 Szukana droga
przebyta przez pręt wynosi
Szukana droga
przebyta przez pręt wynosi
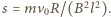 Chwilowe natężenie prądu
indukcyjnego w obwodzie dane jest wzorem
Chwilowe natężenie prądu
indukcyjnego w obwodzie dane jest wzorem
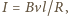 a z definicji
natężenia prądu
a z definicji
natężenia prądu
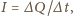 gdzie
gdzie
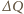 jest ładunkiem
przepływającym w czasie
jest ładunkiem
przepływającym w czasie
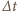 przez opór. Stąd dla krótkich
przedziałów czasowych mamy
przez opór. Stąd dla krótkich
przedziałów czasowych mamy
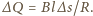 Po zsumowaniu
i uwzględnieniu poprzednich wyników otrzymujemy szukany ładunek równy
Po zsumowaniu
i uwzględnieniu poprzednich wyników otrzymujemy szukany ładunek równy
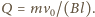
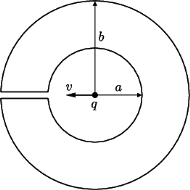
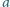 i zewnętrznym
i zewnętrznym
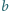 umieszczono cząstkę o masie
umieszczono cząstkę o masie
 naładowaną ładunkiem
naładowaną ładunkiem
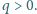 Jaką prędkość należy nadać
cząstce, aby przez wąską szczelinę oddaliła się do nieskończoności?
Przenikalność elektryczna próżni
Jaką prędkość należy nadać
cząstce, aby przez wąską szczelinę oddaliła się do nieskończoności?
Przenikalność elektryczna próżni
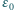 jest dana.
jest dana.
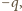 a na powierzchni zewnętrznej
a na powierzchni zewnętrznej
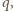 ponieważ
w przewodniku nie ma pola elektrycznego. Energia początkowa układu jest sumą
energii kinetycznej cząstki, energii
ponieważ
w przewodniku nie ma pola elektrycznego. Energia początkowa układu jest sumą
energii kinetycznej cząstki, energii
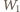 oddziaływania elektrostatycznego
cząstki z ładunkami indukowanymi oraz energii
oddziaływania elektrostatycznego
cząstki z ładunkami indukowanymi oraz energii
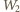 oddziaływania między
ładunkami indukowanymi.
oddziaływania między
ładunkami indukowanymi.
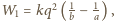 gdzie
gdzie
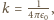
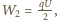 gdzie
gdzie
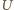 jest napięciem między sferami o promieniach
jest napięciem między sferami o promieniach
 i
i
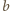 związanym tylko z ładunkami na sferach. Potencjał sfery
wewnętrznej wynosi
związanym tylko z ładunkami na sferach. Potencjał sfery
wewnętrznej wynosi
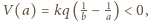 potencjał sfery zewnętrznej
potencjał sfery zewnętrznej
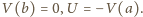 Po oddaleniu się cząstki do nieskończoności
energia układu wynosi zero i z zasady zachowania energii otrzymujemy szukaną
prędkość:
Po oddaleniu się cząstki do nieskończoności
energia układu wynosi zero i z zasady zachowania energii otrzymujemy szukaną
prędkość:
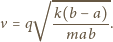
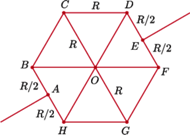
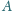 i
i
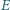 układu
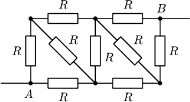
oporników w kształcie sześciokąta foremnego z przekątnymi (rysunek),
zbudowanego z 12 jednakowych elementów, o oporze
układu
oporników w kształcie sześciokąta foremnego z przekątnymi (rysunek),
zbudowanego z 12 jednakowych elementów, o oporze
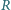 każdy.
każdy.
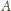 i
i
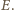 Wynika stąd, że potencjał odpowiadających sobie punktów
leżących powyżej i poniżej tej prostej jest taki sam, tzn.
Wynika stąd, że potencjał odpowiadających sobie punktów
leżących powyżej i poniżej tej prostej jest taki sam, tzn.
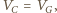
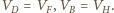 Łącząc punkty o jednakowym potencjale i zastępując
równocześnie opory, które zostaną przy tym połączone równolegle,
dostaniemy obwód zastępczy:
Łącząc punkty o jednakowym potencjale i zastępując
równocześnie opory, które zostaną przy tym połączone równolegle,
dostaniemy obwód zastępczy:
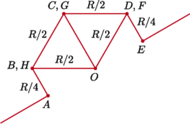
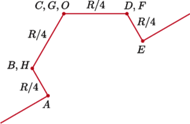
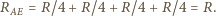

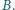 Napięcie między okładkami kondensatora wynosi
Napięcie między okładkami kondensatora wynosi
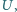 odległość między okładkami
odległość między okładkami
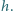 Z punktu
Z punktu
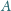 wylatuje
elektron prostopadle do linii pola magnetycznego. Jaki warunek musi spełniać
prędkość elektronu, żeby przeleciał on przez kondensator bez kontaktu z jego
okładkami? Siły ciężkości nie uwzględniamy, efekty relatywistyczne możemy
zaniedbać.
wylatuje
elektron prostopadle do linii pola magnetycznego. Jaki warunek musi spełniać
prędkość elektronu, żeby przeleciał on przez kondensator bez kontaktu z jego
okładkami? Siły ciężkości nie uwzględniamy, efekty relatywistyczne możemy
zaniedbać.
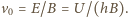 W układzie
W układzie
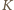 związanym z kondensatorem
elektron porusza się wtedy ruchem prostoliniowym z prędkością
związanym z kondensatorem
elektron porusza się wtedy ruchem prostoliniowym z prędkością
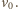 W układzie odniesienia
W układzie odniesienia
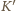 poruszającym się względem
poruszającym się względem
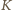 z prędkością
z prędkością
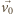 elektron ten spoczywa, czyli siła magnetyczna
na niego nie działa. Oznacza to, że w układzie
elektron ten spoczywa, czyli siła magnetyczna
na niego nie działa. Oznacza to, że w układzie
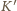 nie może również
działać siła elektryczna, czyli w układzie tym nie ma pola elektrycznego.
Elektron wylatujący z punktu
nie może również
działać siła elektryczna, czyli w układzie tym nie ma pola elektrycznego.
Elektron wylatujący z punktu
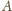 z prędkością
z prędkością
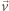 ma w układzie
ma w układzie
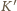 prędkość
prędkość
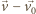 i porusza się po okręgu o promieniu
i porusza się po okręgu o promieniu
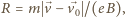 stycznym do prostej równoległej do prędkości
stycznym do prostej równoległej do prędkości
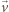 (
(
 i
i
 oznaczają odpowiednio masę i wartość
bezwzględną ładunku elektronu). Ponieważ mamy do czynienia z przypadkiem
nierelatywistycznym, wektor indukcji pola magnetycznego w układzie
oznaczają odpowiednio masę i wartość
bezwzględną ładunku elektronu). Ponieważ mamy do czynienia z przypadkiem
nierelatywistycznym, wektor indukcji pola magnetycznego w układzie
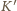 nadal wynosi
nadal wynosi
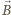 (patrz zadanie 560). W układzie związanym
z kondensatorem ruch elektronu jest złożeniem ruchu po okręgu oraz ruchu
postępowego z prędkością
(patrz zadanie 560). W układzie związanym
z kondensatorem ruch elektronu jest złożeniem ruchu po okręgu oraz ruchu
postępowego z prędkością
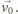 Elektron przeleci przez kondensator bez
kontaktu z okładkami, gdy
Elektron przeleci przez kondensator bez
kontaktu z okładkami, gdy
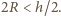 Zatem prędkość elektronu musi
spełniać warunki:
Zatem prędkość elektronu musi
spełniać warunki:
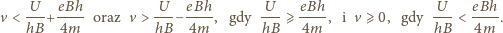
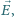 to w układzie poruszającym się z prędkością
to w układzie poruszającym się z prędkością
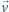 względem
układu pierwotnego, gdy możemy zaniedbać efekty relatywistyczne, istnieje
również pole magnetyczne
względem
układu pierwotnego, gdy możemy zaniedbać efekty relatywistyczne, istnieje
również pole magnetyczne
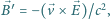 gdzie
gdzie
 jest
prędkością światła. Sprawdź prawdziwość tego stwierdzenia na przykładzie
pola od ładunku punktowego, rozważanego w obu układach.
jest
prędkością światła. Sprawdź prawdziwość tego stwierdzenia na przykładzie
pola od ładunku punktowego, rozważanego w obu układach.
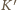 porusza się z prędkością
porusza się z prędkością
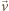 względem układu
inercjalnego
względem układu
inercjalnego
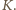 Rozważmy ładunek punktowy
Rozważmy ładunek punktowy
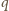 spoczywający
w początku układu
spoczywający
w początku układu
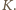 Pole elektryczne od tego ładunku w punkcie opisanym
wektorem położenia
Pole elektryczne od tego ładunku w punkcie opisanym
wektorem położenia
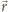 ma postać:
ma postać:
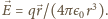 W układzie
W układzie
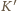 ładunek
ładunek
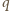 porusza się prędkością
porusza się prędkością
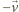 i w przybliżeniu
nierelatywistycznym możemy go potraktować jako stały prąd elektryczny.
Natężenie prądu dane jest wzorem
i w przybliżeniu
nierelatywistycznym możemy go potraktować jako stały prąd elektryczny.
Natężenie prądu dane jest wzorem
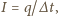 gdzie
gdzie
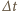 jest
czasem, w którym ładunek przemieszcza się o
jest
czasem, w którym ładunek przemieszcza się o
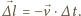 Stąd
Stąd
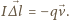 Zgodnie z prawem Biota–Savarta pole magnetyczne
wytworzone w układzie
Zgodnie z prawem Biota–Savarta pole magnetyczne
wytworzone w układzie
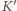 przez poruszający się ładunek ma
postać:
przez poruszający się ładunek ma
postać:
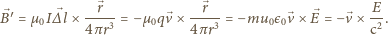
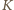 obok pola elektrycznego występuje
również pole magnetyczne
obok pola elektrycznego występuje
również pole magnetyczne
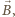 pole magnetyczne w układzie
pole magnetyczne w układzie
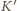 ma postać:
ma postać:
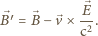
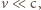 kiedy możemy
zaniedbać opóźnienie związane ze skończonym rozchodzeniem się sygnału
elektromagnetycznego. Otrzymany wzór pokazuje, że w przybliżeniu
nierelatywistycznym pole magnetyczne nie zmienia się przy przejściu z jednego
układu inercjalnego do innego.
kiedy możemy
zaniedbać opóźnienie związane ze skończonym rozchodzeniem się sygnału
elektromagnetycznego. Otrzymany wzór pokazuje, że w przybliżeniu
nierelatywistycznym pole magnetyczne nie zmienia się przy przejściu z jednego
układu inercjalnego do innego.
 nad poziomem wody. Rejestruje on sygnały wysyłane przez satelitę
wznoszącego się nad horyzontem. Przy jakich kątach wzniesienia satelity nad
horyzontem obserwuje się maksima sygnału? Długość fali emitowanej przez
satelitę wynosi
nad poziomem wody. Rejestruje on sygnały wysyłane przez satelitę
wznoszącego się nad horyzontem. Przy jakich kątach wzniesienia satelity nad
horyzontem obserwuje się maksima sygnału? Długość fali emitowanej przez
satelitę wynosi
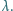 Przyjmujemy, że powierzchnia jeziora jest idealnie
gładka.
Przyjmujemy, że powierzchnia jeziora jest idealnie
gładka.
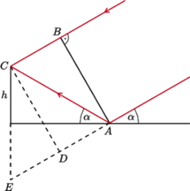
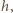 możemy przyjąć, że wiązka promieniowania wysyłanego przez
satelitę jest równoległa. Do odbiornika w punkcie
możemy przyjąć, że wiązka promieniowania wysyłanego przez
satelitę jest równoległa. Do odbiornika w punkcie
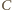 docierają
promienie biegnące bezpośrednio od satelity i odbite od powierzchni
jeziora, jak na rysunku. Punkty
docierają
promienie biegnące bezpośrednio od satelity i odbite od powierzchni
jeziora, jak na rysunku. Punkty
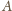 i
i
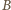 leżą na tej samej
powierzchni falowej i mają zgodną fazę. Ich różnica dróg jest równa
leżą na tej samej
powierzchni falowej i mają zgodną fazę. Ich różnica dróg jest równa
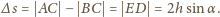 Jeden z promieni odbija się od
ośrodka, w którym prędkość rozchodzenia się fali jest mniejsza niż
w powietrzu. Powoduje to zmianę fazy o
Jeden z promieni odbija się od
ośrodka, w którym prędkość rozchodzenia się fali jest mniejsza niż
w powietrzu. Powoduje to zmianę fazy o
 odpowiadającą przebytej
drodze
odpowiadającą przebytej
drodze
 Uwzględniając to, otrzymujemy wzór na maksima
interferencyjne:
Uwzględniając to, otrzymujemy wzór na maksima
interferencyjne:
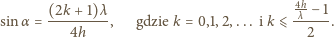
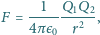 jak
w układzie SI, tylko jako
jak
w układzie SI, tylko jako

 na
jedynkę. Jak dokonać transformacji odwrotnej? Ile wynosi ładunek elementarny
w tych układach?
na
jedynkę. Jak dokonać transformacji odwrotnej? Ile wynosi ładunek elementarny
w tych układach?
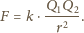
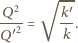
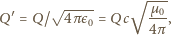
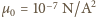 jest przenikalnością magnetyczną próżni.
Podstawiając wartości liczbowe dla ładunku elementarnego, otrzymujemy
jest przenikalnością magnetyczną próżni.
Podstawiając wartości liczbowe dla ładunku elementarnego, otrzymujemy
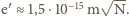
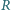 lewituje w nieskończonym
niebieskim pastwisku o temperaturze
lewituje w nieskończonym
niebieskim pastwisku o temperaturze
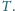 Krowy są dobrymi przewodnikami
elektryczności. Oszacować wielkość ładunku zgromadzonego na
krowie.
Krowy są dobrymi przewodnikami
elektryczności. Oszacować wielkość ładunku zgromadzonego na
krowie.
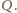 Wytwarza on
pole elektryczne o natężeniu
Wytwarza on
pole elektryczne o natężeniu
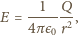
 jest odległością od środka krowy. Gęstość energii pola
elektrycznego wyraża się wzorem
jest odległością od środka krowy. Gęstość energii pola
elektrycznego wyraża się wzorem
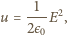
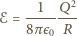
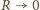 otrzymujemy znany problem nieskończonej energii ładunku
punktowego). Skoro krowa jest elementarna, to z zasady ekwipartycji energii
„należy się” jej
otrzymujemy znany problem nieskończonej energii ładunku
punktowego). Skoro krowa jest elementarna, to z zasady ekwipartycji energii
„należy się” jej
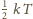 na każdy stopień swobody. Dla ruchu
dwuwymiarowego otrzymujemy więc
na każdy stopień swobody. Dla ruchu
dwuwymiarowego otrzymujemy więc
 co dla
co dla
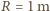 i
i
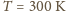 daje
daje
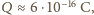 czyli kilka tysięcy
ładunków elementarnych.
czyli kilka tysięcy
ładunków elementarnych.
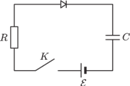
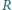 w obwodzie przedstawionym na
rysunku (a) po zamknięciu klucza? W chwili początkowej kondensator
o pojemności
w obwodzie przedstawionym na
rysunku (a) po zamknięciu klucza? W chwili początkowej kondensator
o pojemności
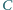 nie jest naładowany. Siła elektromotoryczna źródła
prądu wynosi
nie jest naładowany. Siła elektromotoryczna źródła
prądu wynosi
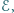 opór wewnętrzny źródła jest zaniedbywalny.
Wyidealizowana charakterystyka prądowo-napięciowa diody przedstawiona jest
na rysunku (b).
opór wewnętrzny źródła jest zaniedbywalny.
Wyidealizowana charakterystyka prądowo-napięciowa diody przedstawiona jest
na rysunku (b).
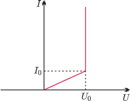
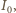 czyli spełniony jest warunek
czyli spełniony jest warunek
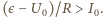 Podczas
ładowania kondensatora natężenie prądu maleje i w pewnym czasie
Podczas
ładowania kondensatora natężenie prądu maleje i w pewnym czasie
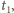 dopóki nie osiągnie wartości
dopóki nie osiągnie wartości
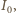 napięcie na diodzie ma
stałą wartość
napięcie na diodzie ma
stałą wartość
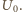 Ładunek, którym naładuje się w tym czasie
kondensator, wynosi
Ładunek, którym naładuje się w tym czasie
kondensator, wynosi
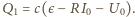 Zgodnie z zasadą zachowania
energii:
Zgodnie z zasadą zachowania
energii:
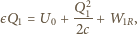
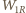 jest ciepłem wydzielonym na oporze
jest ciepłem wydzielonym na oporze
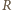 w czasie
w czasie
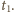 W czasie
W czasie
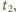 gdy natężenie prądu w obwodzie jest
mniejsze niż
gdy natężenie prądu w obwodzie jest
mniejsze niż
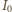 i maleje do zera, napięcie na diodzie maleje liniowo
z natężeniem prądu, czyli jej opór
i maleje do zera, napięcie na diodzie maleje liniowo
z natężeniem prądu, czyli jej opór
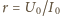 jest stały. Ładunek, który
przepływa w tym czasie w obwodzie, wynosi
jest stały. Ładunek, który
przepływa w tym czasie w obwodzie, wynosi
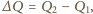 gdzie
końcowy ładunek na kondensatorze to
gdzie
końcowy ładunek na kondensatorze to
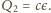 Energia wydzielona
w tym czasie w obwodzie równa jest pracy źródła i wynosi
Energia wydzielona
w tym czasie w obwodzie równa jest pracy źródła i wynosi
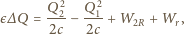
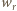 jest ciepłem wydzielonym na diodzie, a
jest ciepłem wydzielonym na diodzie, a
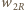 ciepłem
wydzielonym na oporze
ciepłem
wydzielonym na oporze
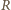 w czasie
w czasie
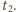 Ponieważ dioda i opornik
są połączone szeregowo i w każdej chwili płynie przez nie prąd o tym samym
natężeniu, zachodzi związek
Ponieważ dioda i opornik
są połączone szeregowo i w każdej chwili płynie przez nie prąd o tym samym
natężeniu, zachodzi związek
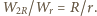 Całkowite ciepło wydzielone
na oporze
Całkowite ciepło wydzielone
na oporze
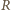 w czasie
w czasie
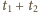 wynosi
wynosi
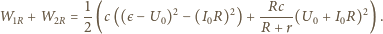
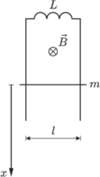
 dołączono do górnych końców dwóch
równoległych szyn przewodzących ustawionych pionowo. Odstęp między
szynami jest równy
dołączono do górnych końców dwóch
równoległych szyn przewodzących ustawionych pionowo. Odstęp między
szynami jest równy
 Jednorodne pole magnetyczne o indukcji
Jednorodne pole magnetyczne o indukcji
 ma kierunek poziomy i jest prostopadłe do płaszczyzny szyn. Poziomy,
przewodzący pręt o masie
ma kierunek poziomy i jest prostopadłe do płaszczyzny szyn. Poziomy,
przewodzący pręt o masie
 może poruszać się w polu magnetycznym
wzdłuż szyn w ten sposób, że stale się z nimi styka. Opór i samoindukcję
przewodników oraz tarcie pręta o szyny zaniedbujemy. Znaleźć zależność
położenia pręta od czasu
może poruszać się w polu magnetycznym
wzdłuż szyn w ten sposób, że stale się z nimi styka. Opór i samoindukcję
przewodników oraz tarcie pręta o szyny zaniedbujemy. Znaleźć zależność
położenia pręta od czasu
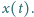 Prędkość początkowa pręta jest równa
zeru.
Prędkość początkowa pręta jest równa
zeru.
 gdzie
gdzie
 jest szybkością zmian położenia pręta. Prąd indukcyjny
płynie w takim kierunku, żeby przeciwdziałać zmianom strumienia pola
magnetycznego, które go wywołują, czyli siła elektrodynamiczna działająca na
pręt ma zwrot przeciwny do siły ciężkości. Równanie ruchu pręta ma
więc postać
jest szybkością zmian położenia pręta. Prąd indukcyjny
płynie w takim kierunku, żeby przeciwdziałać zmianom strumienia pola
magnetycznego, które go wywołują, czyli siła elektrodynamiczna działająca na
pręt ma zwrot przeciwny do siły ciężkości. Równanie ruchu pręta ma
więc postać
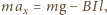 gdzie
gdzie
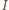 jest natężeniem
prądu w obwodzie. Możemy też napisać drugie prawo Kirchhoffa dla
obwodu zawierającego pręt i cewkę:
jest natężeniem
prądu w obwodzie. Możemy też napisać drugie prawo Kirchhoffa dla
obwodu zawierającego pręt i cewkę:
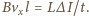 Uwzględniając
warunki początkowe
Uwzględniając
warunki początkowe
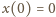 oraz
oraz
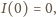 otrzymujemy
otrzymujemy
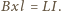 Wstawiając otrzymane stąd wyrażenie na natężenie prądu do
równania ruchu, możemy zapisać je w postaci
Wstawiając otrzymane stąd wyrażenie na natężenie prądu do
równania ruchu, możemy zapisać je w postaci
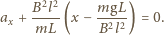
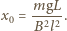
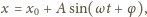 gdzie częstość drgań jest równa
gdzie częstość drgań jest równa
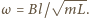 Zależność prędkości od czasu ma postać
Zależność prędkości od czasu ma postać
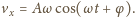 Amplitudę drgań
Amplitudę drgań
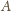 i fazę
początkową
i fazę
początkową
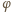 możemy wyznaczyć z warunków początkowych:
możemy wyznaczyć z warunków początkowych:
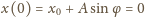 oraz
oraz
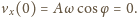 Uwzględniając,
że
Uwzględniając,
że
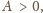 otrzymujemy
otrzymujemy
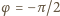 oraz
oraz
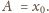 Ostatecznie
zależność położenia pręta od czasu ma postać
Ostatecznie
zależność położenia pręta od czasu ma postać
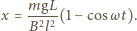
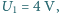 na drugim
oporniku
na drugim
oporniku
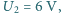 na obu opornikach
na obu opornikach
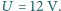 Jakie są
spadki napięć na każdym z oporników, gdy woltomierz nie jest nigdzie
podłączony?
Jakie są
spadki napięć na każdym z oporników, gdy woltomierz nie jest nigdzie
podłączony?
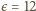 V, jak wynika z trzeciego pomiaru. Oznaczmy opór woltomierza
przez
V, jak wynika z trzeciego pomiaru. Oznaczmy opór woltomierza
przez
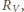 a oporników przez
a oporników przez
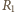 i
i
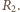 Niech natężenie
prądu płynącego przez opornik
Niech natężenie
prądu płynącego przez opornik
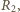 gdy woltomierz połączony jest
równolegle z opornikiem
gdy woltomierz połączony jest
równolegle z opornikiem
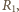 wynosi
wynosi
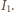 Drugie prawo
Kirchhoffa ma w tym przypadku postać
Drugie prawo
Kirchhoffa ma w tym przypadku postać
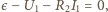 stąd
stąd
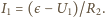 Spadek napięcia na połączonych równolegle opornikach
Spadek napięcia na połączonych równolegle opornikach
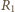 i
i
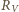 wynosi
wynosi
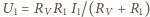 i prowadzi to
do równania
i prowadzi to
do równania
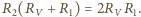 Analogicznie rozważając
przypadek połączenia woltomierza z opornikiem
Analogicznie rozważając
przypadek połączenia woltomierza z opornikiem
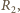 otrzymujemy
równanie
otrzymujemy
równanie
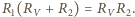 Eliminacja
Eliminacja
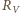 daje związek
daje związek
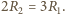 Gdy woltomierz nie jest podłączony, natężenie prądu
w obwodzie wynosi
Gdy woltomierz nie jest podłączony, natężenie prądu
w obwodzie wynosi
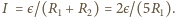 Spadek napięcia na
pierwszym oporniku wynosi więc
Spadek napięcia na
pierwszym oporniku wynosi więc
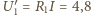 V, na drugim
V, na drugim
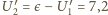 V.
V.
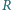 i masie
i masie
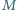 naładowana jest równomiernie ładunkiem
naładowana jest równomiernie ładunkiem
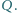 W sferze
znajdują się dwa niewielkie otwory leżące na tej samej średnicy. Cząstka
o masie
W sferze
znajdują się dwa niewielkie otwory leżące na tej samej średnicy. Cząstka
o masie
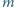 i ładunku
i ładunku
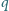 jednoimiennym z
jednoimiennym z
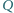 zaczyna
zbliżać się do sfery z bardzo dużej odległości wzdłuż prostej przechodzącej
przez otwory, z prędkością początkową
zaczyna
zbliżać się do sfery z bardzo dużej odległości wzdłuż prostej przechodzącej
przez otwory, z prędkością początkową
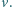 W chwili początkowej sfera
spoczywa. Ile czasu cząstka znajdować się będzie wewnątrz sfery? Przyjmij, że
efekty magnetyczne są zaniedbywalne.
W chwili początkowej sfera
spoczywa. Ile czasu cząstka znajdować się będzie wewnątrz sfery? Przyjmij, że
efekty magnetyczne są zaniedbywalne.
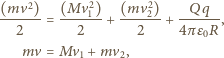
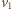 i
i
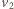 są odpowiednio prędkościami sfery i cząstki
w chwili, gdy cząstka dotrze do pierwszego otworu. Musi być spełniony
warunek
są odpowiednio prędkościami sfery i cząstki
w chwili, gdy cząstka dotrze do pierwszego otworu. Musi być spełniony
warunek
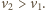 Wiemy z prawa Gaussa, że wewnątrz równomiernie
naładowanej sfery nie ma pola elektrycznego, cząstka porusza się więc od jednego
do drugiego otworu ruchem jednostajnym prostoliniowym z prędkością
względną
Wiemy z prawa Gaussa, że wewnątrz równomiernie
naładowanej sfery nie ma pola elektrycznego, cząstka porusza się więc od jednego
do drugiego otworu ruchem jednostajnym prostoliniowym z prędkością
względną
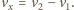 Szukany czas wynosi
Szukany czas wynosi
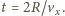
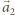 i
i
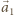 odpowiednio cząstki i sfery w dowolnym
układzie inercjalnym wynoszą
odpowiednio cząstki i sfery w dowolnym
układzie inercjalnym wynoszą
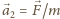 i
i
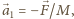 gdzie
gdzie
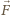 jest siłą, jaką sfera działa na cząstkę wzdłuż wektora położenia
względnego obu ciał, a jej wartość zależy od odległości między
nimi. Przyspieszenie względne wynosi
jest siłą, jaką sfera działa na cząstkę wzdłuż wektora położenia
względnego obu ciał, a jej wartość zależy od odległości między
nimi. Przyspieszenie względne wynosi
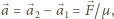 gdzie
gdzie
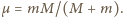 Jest to równanie ruchu fikcyjnej cząstki o masie
Jest to równanie ruchu fikcyjnej cząstki o masie
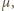 zwanej masą zredukowaną układu dwóch ciał, poruszającej się z ich
prędkością względną w polu siły
zwanej masą zredukowaną układu dwóch ciał, poruszającej się z ich
prędkością względną w polu siły
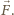 Zasada zachowania energii
w naszym problemie sprowadzonym do ruchu jednego ciała ma teraz
postać
Zasada zachowania energii
w naszym problemie sprowadzonym do ruchu jednego ciała ma teraz
postać
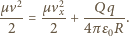
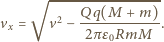
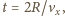 gdy
gdy
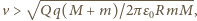 dla
mniejszych prędkości cząstka nie dotrze do wnętrza sfery.
dla
mniejszych prędkości cząstka nie dotrze do wnętrza sfery.
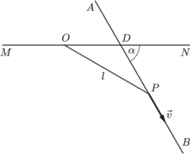
 biegnie ze stałą prędkością
biegnie ze stałą prędkością
 po prostej
po prostej
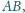 która
tworzy kąt
która
tworzy kąt
 z poziomo rozciągniętym drutem
z poziomo rozciągniętym drutem
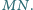 Do
obroży psa przymocowana jest lekka pozioma linka o długości
Do
obroży psa przymocowana jest lekka pozioma linka o długości
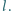 Linka
połączona jest z pierścieniem
Linka
połączona jest z pierścieniem
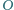 o masie
o masie
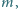 który może
ślizgać się po drucie bez tarcia. Znaleźć naprężenie linki w chwili, gdy pies
i pierścień znajdują się w jednakowych odległościach od punktu przecięcia
który może
ślizgać się po drucie bez tarcia. Znaleźć naprężenie linki w chwili, gdy pies
i pierścień znajdują się w jednakowych odległościach od punktu przecięcia
 prostej
prostej
 i drutu.
i drutu.
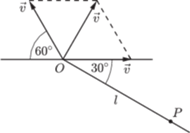
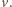 W inercjalnym układzie
odniesienia związanym z psem pierścień porusza się po okręgu o promieniu
W inercjalnym układzie
odniesienia związanym z psem pierścień porusza się po okręgu o promieniu
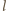 z prędkością chwilową
z prędkością chwilową
 (
(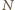 i siła reakcji drutu
i siła reakcji drutu
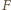 (
(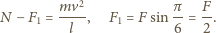
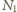 siły naciągu linki równoważy siłę
reakcji
siły naciągu linki równoważy siłę
reakcji
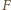 :
:

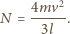
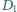 ma
indukcyjność
ma
indukcyjność
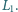 Po podłączeniu cewki do źródła prądu wewnątrz
niej zostało wyindukowane pole magnetyczne o indukcji
Po podłączeniu cewki do źródła prądu wewnątrz
niej zostało wyindukowane pole magnetyczne o indukcji
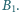 Następnie
cewka została nakręcona na inny rdzeń o średnicy
Następnie
cewka została nakręcona na inny rdzeń o średnicy
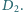 Indukcyjność
cewki była wtedy równa
Indukcyjność
cewki była wtedy równa
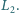 Wyznaczyć indukcję pola magnetycznego
Wyznaczyć indukcję pola magnetycznego
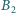 wewnątrz nowej cewki po podłączeniu do tego samego źródła
prądu. Założyć, że przewodnik, z którego jest zrobiona cewka, jest dużo
dłuższy niż długość cewki.
wewnątrz nowej cewki po podłączeniu do tego samego źródła
prądu. Założyć, że przewodnik, z którego jest zrobiona cewka, jest dużo
dłuższy niż długość cewki.
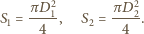
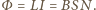 Stąd
Stąd
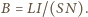 Zatem
Zatem
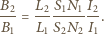
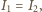 więc
więc
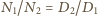 i
i
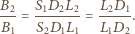
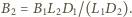
 i
i
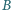 układu pokazanego na
rysunku?
układu pokazanego na
rysunku?
 i
i
 mamy
mamy
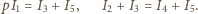
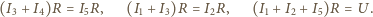
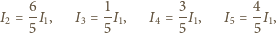
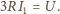
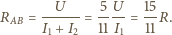
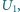 a obwód wtórny był otwarty, napięcie na uzwojeniu
wtórnym było równe
a obwód wtórny był otwarty, napięcie na uzwojeniu
wtórnym było równe
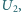 a natężenie prądu w uzwojeniu pierwotnym
a natężenie prądu w uzwojeniu pierwotnym
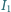 (wszystkie podane wielkości są wartościami skutecznymi).
Zamknięto obwód wtórny, dołączając do niego: a) opornik, b) zwojnicę
bezoporową, c) kondensator. Ile w każdym z tych przypadków wyniesie
natężenie prądu w uzwojeniu pierwotnym, jeśli we wtórnym popłynie prąd
o natężeniu
(wszystkie podane wielkości są wartościami skutecznymi).
Zamknięto obwód wtórny, dołączając do niego: a) opornik, b) zwojnicę
bezoporową, c) kondensator. Ile w każdym z tych przypadków wyniesie
natężenie prądu w uzwojeniu pierwotnym, jeśli we wtórnym popłynie prąd
o natężeniu
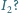 Oba napięcia
Oba napięcia
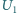 i
i
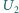 nie zmieniły
wartości, a straty energii w transformatorze (jego nagrzewanie się) można
pominąć.
nie zmieniły
wartości, a straty energii w transformatorze (jego nagrzewanie się) można
pominąć.
 i
i
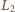 indukcyjności uzwojenia pierwotnego
i wtórnego, a przez
indukcyjności uzwojenia pierwotnego
i wtórnego, a przez
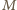 współczynnik indukcji wzajemnej. Równania
wyrażające II prawo Kirchhoffa dla obu obwodów przybierają postać
współczynnik indukcji wzajemnej. Równania
wyrażające II prawo Kirchhoffa dla obu obwodów przybierają postać
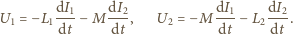
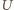 i
i
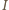 oznaczają –
niezbyt konsekwentnie – wartości chwilowe, w odróżnieniu od dalszych
przekształceń i treści zadania.
oznaczają –
niezbyt konsekwentnie – wartości chwilowe, w odróżnieniu od dalszych
przekształceń i treści zadania.
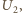 mimo zamknięcia obwodu wtórnego,
świadczy o tym, że sprzężenie indukcyjne obwodów jest maksymalne,
tzn.
mimo zamknięcia obwodu wtórnego,
świadczy o tym, że sprzężenie indukcyjne obwodów jest maksymalne,
tzn.
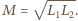 Wtedy stosunek
Wtedy stosunek
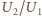 jest równy
jest równy
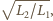 zatem stały. Przyjmując częstość
zatem stały. Przyjmując częstość
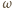 jako daną,
z danych wartości
jako daną,
z danych wartości
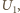
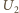 i
i
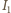 wyznaczamy (dla
wyznaczamy (dla
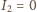 )
)
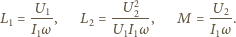
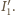 W przypadku a) należy
przyrównać
W przypadku a) należy
przyrównać
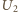 do
do
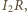 co po wyeliminowaniu przesunięcia
fazy między
co po wyeliminowaniu przesunięcia
fazy między
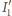 a
a
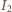 prowadzi do tożsamości
prowadzi do tożsamości
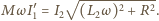
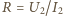 oraz
wyrażeń na
oraz
wyrażeń na
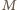 i
i
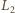 daje szukane natężenie prądu w uzwojeniu
pierwotnym
daje szukane natężenie prądu w uzwojeniu
pierwotnym
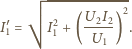
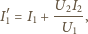
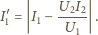
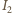 )
we wszystkich przypadkach przechodzimy do powszechnie znanego
związku
)
we wszystkich przypadkach przechodzimy do powszechnie znanego
związku
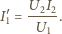
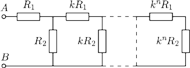
 razy większy niż w poprzednim.
Znaleźć opór między punktami
razy większy niż w poprzednim.
Znaleźć opór między punktami
 i
i
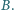 Opory w pierwszym
oczku sieci wynoszą
Opory w pierwszym
oczku sieci wynoszą
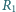 oraz
oraz
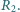
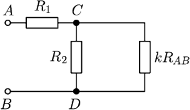
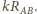 Zatem można przedstawić go
w postaci pokazanej na rysunku obok. Stąd wynika, że
Zatem można przedstawić go
w postaci pokazanej na rysunku obok. Stąd wynika, że
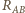 spełnia
równanie:
spełnia
równanie:
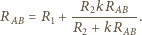
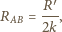

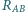 między punktami
między punktami
 i
i
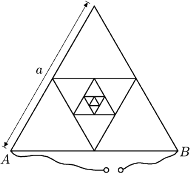
 układu zbudowanego z cienkiej przewodzącej siatki. Przyjąć, że liczba
zmniejszających się oczek siatki jest bardzo duża. Długość boku trójkąta jest
równa
układu zbudowanego z cienkiej przewodzącej siatki. Przyjąć, że liczba
zmniejszających się oczek siatki jest bardzo duża. Długość boku trójkąta jest
równa
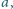 a gęstość liniowa drutu, z którego zrobiona jest siatka,
wynosi
a gęstość liniowa drutu, z którego zrobiona jest siatka,
wynosi
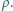
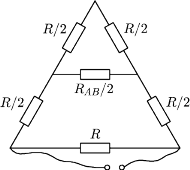
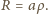 „Wewnętrzny”
układ składa się z nieskończonej ilości oczek, a jego opór wynosi
„Wewnętrzny”
układ składa się z nieskończonej ilości oczek, a jego opór wynosi
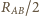 (z symetrii układu). Zatem
(z symetrii układu). Zatem
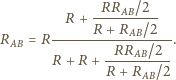
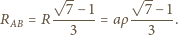
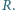 Odczytano wskazanie amperomierza
Odczytano wskazanie amperomierza
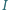 dla różnych
wartości
dla różnych
wartości
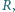 a wyniki przedstawiono w tabeli:
a wyniki przedstawiono w tabeli: 
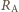 będzie szukanym oporem amperomierza, a
będzie szukanym oporem amperomierza, a
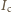 – natężeniem
prądu całkowitego, czyli sumą natężenia prądu płynącego przez
amperomierz
– natężeniem
prądu całkowitego, czyli sumą natężenia prądu płynącego przez
amperomierz
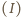 i przez bocznik. Napięcie na amperomierzu i boczniku
jest jednakowe, zatem
i przez bocznik. Napięcie na amperomierzu i boczniku
jest jednakowe, zatem
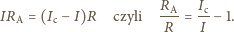
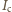 jest stałe, to wykres zależności
jest stałe, to wykres zależności
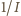 od
od
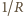 powinien
być liniowy, co dla danej serii pomiarów sprawdza się bardzo dobrze.
Z ekstrapolacji prostej do przecięcia z osią
powinien
być liniowy, co dla danej serii pomiarów sprawdza się bardzo dobrze.
Z ekstrapolacji prostej do przecięcia z osią
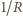 (tzn. do punktu,
w którym
(tzn. do punktu,
w którym
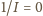 ) znajdujemy
) znajdujemy