Skrót regulaminu

Każdy może nadsyłać rozwiązania zadań z numeru w terminie do końca miesiąca 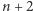. Szkice rozwiązań zamieszczamy w numerze 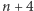. Można nadsyłać rozwiązania czterech, trzech, dwóch lub jednego zadania, można to robić co miesiąc lub z dowolnymi przerwami. Rozwiązanie każdego zadania powinno być pisane na oddzielnym arkuszu papieru oraz podpisane imieniem i nazwiskiem. Uczniowie proszeni są o podanie klasy, studenci -roku i uczelni. Rozwiązania zadań z matematyki i z fizyki należy przysyłać w oddzielnych kopertach, z dopiskiem na kopercie: Klub 44 M lub Klub 44 F. Można także przysyłać je pocztą elektroniczną pod adresem delta@mimuw.edu.pl. Oceniamy zadania w skali od 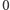do 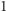z dokładnością do 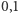. Ocenę mnożymy przez współczynnik trudności danego zadania: 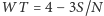, gdzie 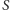oznacza sumę ocen za rozwiązania tego zadania, a 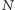- liczbę osób, które nadesłały rozwiązanie choćby jednego zadania z danego numeru w danej konkurencji ( M lub F) - i tyle punktów otrzymuje nadsyłający. Po zgromadzeniu 44 punktów, w dowolnym czasie i w którejkolwiek z dwóch konkurencji ( M lub F), zostaje on członkiem Klubu 44, a nadwyżka punktów jest zaliczana do ponownego udziału. Trzykrotne członkostwo - to tytuł Weterana.
Szczegółowy regulamin

---

Termin nadsyłania rozwiązań: 30 IV 2018

Rozwiązania zadań z numeru 10/2017

***

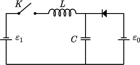
Na początku wyrazy skruchy.
Na rysunku do treści zadania 636 odwrotnie zaznaczony został kierunek przewodzenia diody. Rozwiązanie zamieszczone w sierpniowym numerze Delty jest zgodne z rysunkiem zamieszczonym w niniejszym podsumowaniu. Prąd zaczyna płynąć przez źródło o sile elektromotorycznej 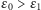dopiero wtedy, gdy napięcie na kondensatorze przewyższa 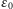i to było istotą zadania. Błędny rysunek spowodował, że zadanie straciło sens, a szkoda, bo wydawało się dosyć interesujące. Większość uczestników zbojkotowała je bez komentarza. Początek jednego z nadesłanych rozwiązań sugerował, że autor milcząco zmienił rysunek na prawidłowy, ale przedstawione rozumowanie nie doprowadziło do pomyślnego finału. W tej sytuacji zadanie zostało unieważnione, a za zaistniałą sytuację wszystkich Czytelników bardzo przepraszam.

Najtrudniejsze w tym roku okazało się zadanie 625 (WT=3,6) z elektrostatyki, w którym trzeba było obliczyć, o ile podnosi się ciecz dielektryczna, pod którą umieszczona jest naładowana płytka. Próby rozwiązania tego zadania podjęły tylko dwie osoby i były to rozwiązania obarczone istotnymi błędami. Współczynnik trudności WT=3,55 miało zadanie 633 z optyki, gdzie należało wyznaczyć ogniskową zwierciadła sferycznego w układzie optycznym z soczewką rozpraszającą. Jedynym uczestnikiem, który przysłał rozwiązanie tego zadania i w dodatku poprawne, był pan Jan Zambrzycki. W zadaniu 628 z mechaniki, o takim samym WT, pytanie było o minimalną prędkość początkową żaby skaczącej przez półwalec. Większość klubowiczów przyjęła tu nieprawdziwe założenie, że punkt styczności żaby z półwalcem powinien znajdować się w najwyższym punkcie półwalca. Autorem poprawnego rozwiązania z pełną dyskusją był pan Tomasz Wietecha. Pan Tomasz jako jedyny rozwiązał też bezbłędnie zadanie 631 (WT=3,5) na temat zderzenia sprężystego walców.

Kolejne miejsca w rankingu stopnia trudności zajęły zadania z mechaniki: 622 (WT=3,4) i 635 (WT=3,35). W pierwszym motocyklista miał rozpędzić się na torze kołowym, optymalnie wykorzystując siłę tarcia. Niektórzy uczestnicy nie uwzględniali tu faktu, że przy rozpędzaniu tarcie musi mieć zarówno składową dośrodkową, jak i styczną do toru, co było sporym zaskoczeniem. W drugim zadaniu należało wyznaczyć stan równowagi wahadła z tarciem. I znowu maksymalną liczbę punktów w obu przypadkach zdobył tu pan Wietecha, mistrz w rozwiązywaniu zadań z mechaniki.

W zadaniu 627 (WT=3,18) z termodynamiki trzeba było znaleźć przyrost energii wewnętrznej gazu w izolowanym cieplnie naczyniu po obciążeniu tłoka dodatkowym ciężarkiem. Mimo że był to proces nieodwracalny, większość klubowiczów stosowała tu równanie przemiany adiabatycznej odwracalnej. Tego samego typu błędy pojawiły się rok temu, przy okazji zadania 595.

Ciekawostką jest pochodzenie zadania 624 (WT=2,5), w którym należało wyznaczyć najmniejszą długość sprężyny obciążonej ciężarkiem spadającym w polu ciężkości po odchyleniu jej do poziomu i rozciągnięciu. Rozwiązywali je moi uczniowie na egzaminie do Cambridge. Udało się im to dopiero po powrocie do Warszawy, ale na uczelnię zostali przyjęci. W Klubie rozwiązali je poprawnie pan Marian Łupieżowiec i znowu pan Wietecha, który w tym roku po raz 12 zdobył 44 punkty.