Skrót regulaminu

Każdy może nadsyłać rozwiązania zadań z numeru w terminie do końca miesiąca 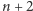. Szkice rozwiązań zamieszczamy w numerze 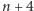. Można nadsyłać rozwiązania czterech, trzech, dwóch lub jednego zadania, można to robić co miesiąc lub z dowolnymi przerwami. Rozwiązanie każdego zadania powinno być pisane na oddzielnym arkuszu papieru oraz podpisane imieniem i nazwiskiem. Uczniowie proszeni są o podanie klasy, studenci -roku i uczelni. Rozwiązania zadań z matematyki i z fizyki należy przysyłać w oddzielnych kopertach, z dopiskiem na kopercie: Klub 44 M lub Klub 44 F. Można także przysyłać je pocztą elektroniczną pod adresem delta@mimuw.edu.pl. Oceniamy zadania w skali od 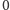do 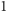z dokładnością do 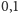. Ocenę mnożymy przez współczynnik trudności danego zadania: 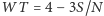, gdzie 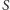oznacza sumę ocen za rozwiązania tego zadania, a 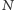- liczbę osób, które nadesłały rozwiązanie choćby jednego zadania z danego numeru w danej konkurencji ( M lub F) - i tyle punktów otrzymuje nadsyłający. Po zgromadzeniu 44 punktów, w dowolnym czasie i w którejkolwiek z dwóch konkurencji ( M lub F), zostaje on członkiem Klubu 44, a nadwyżka punktów jest zaliczana do ponownego udziału. Trzykrotne członkostwo - to tytuł Weterana.
Szczegółowy regulamin

Termin nadsyłania rozwiązań: 30 IV 2015

Rozwiązania zadań z numeru 10/2014

W ubiegłym roku najtrudniejsze okazało się zadanie 570, gdzie należało znaleźć przyspieszenie pręta poruszającego się w rurze z wodą. Jego współczynnik trudności wyniósł 3,90. Gdy pręt podnosi się, pewna masa wody porusza się do dołu, zapełniając oswobodzone miejsce. Siła działająca na pręt ze strony wody zależy od przyspieszenia tej wody. Prawo Archimedesa w postaci: siła wyporu równa jest ciężarowi wypartej cieczy, nie ma w tym przypadku zastosowania, a tak właśnie próbowali rozwiązać zadanie uczestnicy klubu. Trudne okazało się też zadanie 563(WT=3,40), które zresztą, jak słusznie wytknął mi Andrzej Idzik, pojawiło się już w Delcie w 1986 r. Trzeba było w nim obliczyć prędkość, jaką należy nadać ładunkowi punktowemu w środku wydrążonej metalowej kuli, aby oddalił się do nieskończoności przez wąską szczelinę w tej kuli. W nadesłanych rozwiązaniach uwzględniano na ogół oddziaływanie ładunku punktowego z ładunkami indukowanymi na powierzchniach kuli, natomiast nie uwzględniano oddziaływania między ładunkami indukowanymi na obu powierzchniach. W zadaniu 577, odpowiadając na pytanie, jaką prędkość uzyska walec po wyłączeniu pola magnetycznego, w którym był umieszczony, rozwiązujący zaniedbali zjawisko samoindukcji. Zadanie 575 (wciąganie cieczy dielektrycznej do kondensatora) część klubowiczów rozwiązała poprawnie, poszukując minimum energii takiego układu, część jednak uznała, że przyrost energii potencjalnej grawitacji rekompensowany jest obniżeniem energii elektrostatycznej, powtarzając błąd szeroko dyskutowany po jednej z matur jeszcze przed reformą. Niektóre błędy trzymają się więc mocno. Zadanie 576, gdzie klocki połączone sprężyną zsuwały się z równi, dwóch uczestników rozwiązało w układzie związanym z równią, wykazując się imponującą sprawnością rachunkową. Warto jednak było zrobić to w układzie związanym ze środkiem masy, co zdecydowanie upraszczało obliczenia i pozwalało łatwiej uchwycić istotę tego ruchu.

Dziękuję wszystkim, którzy nadsyłali rozwiązania, zapewniając mi sprzężenie zwrotne, przepraszam za niedociągnięcia i literówki, których nie udało się uniknąć. Podobnie jak w roku ubiegłym, wyrażam szczególne uznanie za sposób prezentacji na ogół bezbłędnych rozwiązań i ich dyskusję przez Tomasza Wietechę.