Wierzchołki, krawędzie, ściany i dalej
Zajmijmy się następującym prostym problemem. Niech 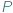 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 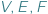 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 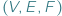 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
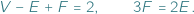 |

Czworościan foremny i dwudziestościan foremny to przykłady wielościanów symplicjalnych
Pierwsza z nich to słynny wzór Eulera, druga zaś bierze się z wyliczenia na dwa sposoby liczby par (Krawędź, Ściana), gdzie Krawędź należy do Ściany. Stąd szybko dostajemy, że 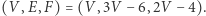 Ponadto
Ponadto 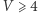 (w przeciwnym razie "wielościan" byłby figurą płaską). Okazuje się, że te dwa ograniczenia są już wystarczające, aby wektor
(w przeciwnym razie "wielościan" byłby figurą płaską). Okazuje się, że te dwa ograniczenia są już wystarczające, aby wektor  pochodził od pewnego wielościanu z trójkątnymi ścianami. Wnikliwego Czytelnika zachęcamy do skonstruowania odpowiednich przykładów.
pochodził od pewnego wielościanu z trójkątnymi ścianami. Wnikliwego Czytelnika zachęcamy do skonstruowania odpowiednich przykładów.
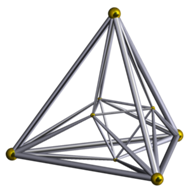
Wikimedia Commons contributors
Szkielet 16-komórki, czyli 4-wymiarowego odpowiednika ośmiościanu foremnego
To oczywiście nie koniec zabawy. Załóżmy, że zamiast wielościanu rozpatrujemy jego wyżej wymiarowy odpowiednik (wielotop) 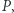 którego ściany są sympleksami (czyli wyżej wymiarowymi odpowiednikami trójkątów, takimi jak trójwymiarowy czworościan) - innymi słowy, wielotop
którego ściany są sympleksami (czyli wyżej wymiarowymi odpowiednikami trójkątów, takimi jak trójwymiarowy czworościan) - innymi słowy, wielotop 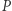 jest symplicjalny. Dla
jest symplicjalny. Dla 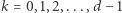 oznaczmy przez
oznaczmy przez 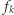 liczbę
liczbę 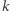 -wymiarowych ścian wielotopu
-wymiarowych ścian wielotopu  - a więc
- a więc 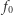 to liczba wierzchołków,
to liczba wierzchołków, 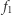 to liczba krawędzi i tak dalej. Otrzymujemy wtedy f-wektor wielotopu
to liczba krawędzi i tak dalej. Otrzymujemy wtedy f-wektor wielotopu 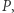 czyli
czyli 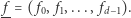 Chcielibyśmy dowiedzieć się, które wektory (o współrzędnych naturalnych) możemy uzyskać jako f-wektory wielotopów symplicjalnych.
Chcielibyśmy dowiedzieć się, które wektory (o współrzędnych naturalnych) możemy uzyskać jako f-wektory wielotopów symplicjalnych.
Powyżej uzyskane dla 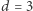 warunki możemy bez trudu uogólnić. Dla przykładu, jeśli wielotop jest czterowymiarowy, wzór Eulera przyjmuje postać
warunki możemy bez trudu uogólnić. Dla przykładu, jeśli wielotop jest czterowymiarowy, wzór Eulera przyjmuje postać 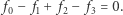 Z kolei zamiast powyższej równości
Z kolei zamiast powyższej równości 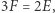 w analogiczny sposób dostajemy równość
w analogiczny sposób dostajemy równość 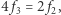 a więc
a więc 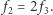 Stąd
Stąd
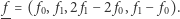 |
Ponadto, podobnie jak poprzednio, mamy ograniczenie 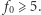 Ale skoro
Ale skoro  to również
to również 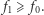 Okazuje się jednak, że zachodzi dużo silniejsza nierówność, mianowicie
Okazuje się jednak, że zachodzi dużo silniejsza nierówność, mianowicie 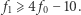 Te warunki wystarczają już, aby dany wektor liczb naturalnych był f-wektorem pewnego czterowymiarowego wielotopu symplicjalnego.
Te warunki wystarczają już, aby dany wektor liczb naturalnych był f-wektorem pewnego czterowymiarowego wielotopu symplicjalnego.
Widać jednak, że wraz ze wzrostem liczby wymiarów konieczne warunki stają się coraz bardziej skomplikowane. Czy możemy liczyć na jakiś opis możliwych f-wektorów w ogólnym przypadku?
Spójrzmy, jak wcześniejsze warunki uogólniają się na dowolną liczbę wymiarów. Wzór Eulera w wyższych wymiarach mówi, że
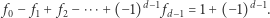 |
Mamy również analogiczne zależności 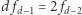 oraz
oraz 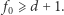 Ponadto, jeśli
Ponadto, jeśli  to w każdym
to w każdym 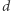 -wymiarowym wielotopie zachodzi nierówność
-wymiarowym wielotopie zachodzi nierówność 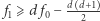 (dla
(dla 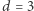 zachodzi nawet równość, co pokazaliśmy w drugim akapicie). Ta nietrywialna nierówność, znana wcześniej jako hipoteza o dolnym ograniczeniu, została udowodniona w 1970 roku przez Davida Barnette. Ale okazuje się, że w ogólności warunków (zarówno nierówności, jak i równości) jest więcej.
zachodzi nawet równość, co pokazaliśmy w drugim akapicie). Ta nietrywialna nierówność, znana wcześniej jako hipoteza o dolnym ograniczeniu, została udowodniona w 1970 roku przez Davida Barnette. Ale okazuje się, że w ogólności warunków (zarówno nierówności, jak i równości) jest więcej.
Dla dowolnego  -wymiarowego wielotopu zdefiniujmy h-wektor jako
-wymiarowego wielotopu zdefiniujmy h-wektor jako 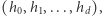 gdzie
gdzie
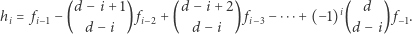 |
Przyjmujemy tutaj konwencję, zgodnie z którą 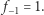 Dla przykładu, jeśli mamy do czynienia z ośmiościanem foremnym, to
Dla przykładu, jeśli mamy do czynienia z ośmiościanem foremnym, to  i dostajemy
i dostajemy
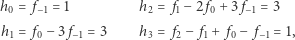 |
a więc h-wektor to 
Ośmiościan foremny
Okazuje się, że dla dowolnego symplicjalnego wielotopu tak otrzymany h-wektor zawsze jest symetryczny! Innymi słowy,  dla
dla 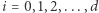 (np. równość
(np. równość 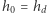 to po prostu wzór Eulera). Równości te nazywane są równaniami Dehna-Sommerville'a i zostały udowodnione już w latach dwudziestych XX wieku. Ponadto można udowodnić, że pierwsza połowa h-wektora tworzy ciąg niemalejący (a druga, na mocy symetrii, tworzy ciąg nierosnący). To twierdzenie jest uogólnieniem hipotezy o dolnym ograniczeniu, która w tym języku mówi po prostu, że
to po prostu wzór Eulera). Równości te nazywane są równaniami Dehna-Sommerville'a i zostały udowodnione już w latach dwudziestych XX wieku. Ponadto można udowodnić, że pierwsza połowa h-wektora tworzy ciąg niemalejący (a druga, na mocy symetrii, tworzy ciąg nierosnący). To twierdzenie jest uogólnieniem hipotezy o dolnym ograniczeniu, która w tym języku mówi po prostu, że 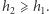
Przedstawione własności to ciągle za mało - istnieją spełniające je ciągi, które nie są f-wektorami żadnego wielotopu. Do sformułowania ostatecznej charakteryzacji przyda się nam następujący lemat:
Lemat. Niech 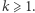 Dla dowolnego
Dla dowolnego 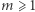 istnieją liczby
istnieją liczby  takie, że
takie, że
 |
ponadto są one wyznaczone jednoznacznie.
Dowód pozostawiamy Czytelnikowi Dociekliwemu jako ćwiczenie. Polecamy zastosowanie indukcji względem  - podstawa indukcji jest trywialna, a w kroku indukcyjnym przyda się znana równość
- podstawa indukcji jest trywialna, a w kroku indukcyjnym przyda się znana równość
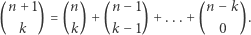 |
Zdefiniujmy teraz 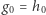 oraz
oraz 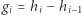 dla
dla 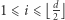 (zauważmy, że
(zauważmy, że 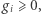 skoro pierwsza połowa h-wektora tworzy ciąg niemalejący). Ustalmy
skoro pierwsza połowa h-wektora tworzy ciąg niemalejący). Ustalmy 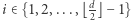 i zgodnie z lematem zapiszmy
i zgodnie z lematem zapiszmy
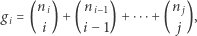 |
gdzie 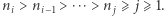 Oznaczmy
Oznaczmy
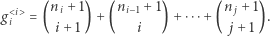 |
Rozważania z zakresu geometrii algebraicznej prowadzą do wniosku, że 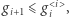 co może się wydawać na pierwszy rzut oka szokujące.
co może się wydawać na pierwszy rzut oka szokujące.
Zależność tę udowodnił Richard Stanley w 1980 roku, a szkic jego rozumowania podajemy na końcu artykułu. Wcześniej w tym samym roku Louis Billera i Carl Lee udowodnili, że tak uzyskane warunki są wystarczające, tzn. że każdy spełniający je ciąg jest f-wektorem pewnego wielotopu. W ten sposób dochodzimy do następującego twierdzenia, dającego ostateczną odpowiedź na postawiony przez nas problem.
Twierdzenie. Wektor  liczb naturalnych jest f-wektorem pewnego wielotopu symplicjalnego wtedy i tylko wtedy, gdy uzyskany z niego h-wektor jest symetryczny, a g-wektor ma współrzędne nieujemne i spełnia nierówności
liczb naturalnych jest f-wektorem pewnego wielotopu symplicjalnego wtedy i tylko wtedy, gdy uzyskany z niego h-wektor jest symetryczny, a g-wektor ma współrzędne nieujemne i spełnia nierówności 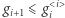 dla
dla 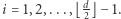
Jeśli będziemy rozważać wszystkie wielotopy (bez ograniczania się do wielotopów symplicjalnych), to g-wektor nadal będzie miał współrzędne nieujemne. Jednak wciąż pozostaje problem otwarty: czy musi on spełniać powyższe nierówności? W ogólnym przypadku definicje h-wektora i g-wektora (zwanych wówczas h-wektorem torycznym i g-wektorem torycznym) muszą jednak zostać zmodyfikowane i są bardziej skomplikowane (w przypadku symplicjalnym pokrywają się z definicjami podanymi powyżej).
***
Szkic dowodu Stanleya
Twierdzenie. Przy oznaczeniach z artykułu zachodzi  dla
dla 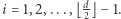
Szkic dowodu. Każdemu wielotopowi, którego wierzchołki mają współrzędne całkowite, możemy przyporządkować pewną rzutową zespoloną rozmaitość algebraiczną (w prostszych słowach - jest to podzbiór zespolonej przestrzeni rzutowej określony pewnym układem równań wielomianowych). Jest to rozmaitość toryczna danego wielotopu.
Wbrew nazwie, nie zawsze jest to rozmaitość w sensie topologicznym. Jednakże jeśli wielotop jest wymiaru 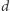 i każdy jego wierzchołek sąsiaduje z dokładnie
i każdy jego wierzchołek sąsiaduje z dokładnie 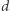 innymi wierzchołkami (taki wielotop nazywamy prostym), to uzyskana rozmaitość może się okazać rozmaitością gładką, a w najgorszym razie będzie orbifoldem (jest to coś na kształt "rozmaitości z rogami").
innymi wierzchołkami (taki wielotop nazywamy prostym), to uzyskana rozmaitość może się okazać rozmaitością gładką, a w najgorszym razie będzie orbifoldem (jest to coś na kształt "rozmaitości z rogami").
Jeśli teraz umieścimy wielotop symplicjalny 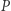 w przestrzeni tak, aby jego wierzchołki miały współrzędne wymierne (to zawsze da się zrobić, jeśli wielotop jest symplicjalny, ale w ogólności nie!), to wielotop dualny (zwany również polarnym) będzie prosty, a jego wierzchołki będą miały współrzędne wymierne. Zatem przekształcając go jednokładnie dostaniemy wielotop o wierzchołkach o współrzędnych całkowitych. Następnie z tego wielotopu otrzymamy pewien orbifold toryczny. Jak ta konstrukcja ma się do f-wektora lub h-wektora? Okazuje się, że współrzędne h-wektora to dokładnie wymiary grup kohomologii (liczby Bettiego) uzyskanej rozmaitości! Co więcej, dowodząc tego faktu, można dowiedzieć się trochę więcej o pierścieniu kohomologii (dokładnie: pierścień kohomologii jest generowany przez
w przestrzeni tak, aby jego wierzchołki miały współrzędne wymierne (to zawsze da się zrobić, jeśli wielotop jest symplicjalny, ale w ogólności nie!), to wielotop dualny (zwany również polarnym) będzie prosty, a jego wierzchołki będą miały współrzędne wymierne. Zatem przekształcając go jednokładnie dostaniemy wielotop o wierzchołkach o współrzędnych całkowitych. Następnie z tego wielotopu otrzymamy pewien orbifold toryczny. Jak ta konstrukcja ma się do f-wektora lub h-wektora? Okazuje się, że współrzędne h-wektora to dokładnie wymiary grup kohomologii (liczby Bettiego) uzyskanej rozmaitości! Co więcej, dowodząc tego faktu, można dowiedzieć się trochę więcej o pierścieniu kohomologii (dokładnie: pierścień kohomologii jest generowany przez 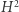 ). Czytelnik zaznajomiony z topologią algebraiczną może dostrzec, że równania Dehna-Sommerville'a to po prostu dualność Poincarégo!
). Czytelnik zaznajomiony z topologią algebraiczną może dostrzec, że równania Dehna-Sommerville'a to po prostu dualność Poincarégo!
Odpowiednie geometryczne twierdzenia pokazują też, że dla orbifoldów torycznych zachodzi tzw. trudne twierdzenie Lefschetza, znane z geometrii rozmaitości zespolonych. Daje to element 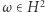 taki, że jeśli podzielimy przezeń pierścień kohomologii, otrzymujemy algebrę z gradacją, w której wymiary kolejnych gradacji to dokładnie
taki, że jeśli podzielimy przezeń pierścień kohomologii, otrzymujemy algebrę z gradacją, w której wymiary kolejnych gradacji to dokładnie 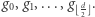 Do tego wiemy, że jest ona generowana przez
Do tego wiemy, że jest ona generowana przez 
Abstrakcyjny algebraiczny rezultat, który jako pierwszy udowodnił Macaulay w 1927, mówi, że taka sytuacja jest możliwa tylko wtedy, gdy 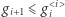 dla
dla 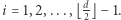
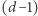 -wymiarowych ścian, suma po lewej stronie zmaleje o
-wymiarowych ścian, suma po lewej stronie zmaleje o 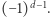 Jeśli będziemy teraz w odpowiedniej kolejności usuwać kolejne
Jeśli będziemy teraz w odpowiedniej kolejności usuwać kolejne 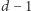 -wymiarowe ściany (za każdym razem usuwając niżej wymiarowe ściany, które nie są już zawarte w żadnej
-wymiarowe ściany (za każdym razem usuwając niżej wymiarowe ściany, które nie są już zawarte w żadnej 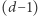 -wymiarowej ścianie), to za każdym razem suma po lewej stronie wzoru Eulera pozostanie niezmieniona. Na końcu zaś, gdy usuniemy ostatnią ścianę, suma zmaleje dokładnie o 1.
-wymiarowej ścianie), to za każdym razem suma po lewej stronie wzoru Eulera pozostanie niezmieniona. Na końcu zaś, gdy usuniemy ostatnią ścianę, suma zmaleje dokładnie o 1.