Mała Delta
Niemożliwe!
- Lolek, chodź, pokażę Ci jedną stronę w Internecie...
- No, co tam masz? Bolek, wyłącz tego Reksia. Mama mówiła, że nie wolno nam oglądać konkurencji!
- Nie, nie to. Tutaj, w drugiej zakładce. Ktoś na tym forum napisał fajne zadanie. Czytaj.
- Jeżeli sześcian w przestrzeni ma wszystkie wierzchołki w punktach kratowych, to jego krawędź ma całkowitą długość.
Zacząłbyś czytać jakieś porządne fora. Przecież to jest oczywista bzdura.
- Niby czemu?
- Bolek, nie widzisz, skąd to się wzięło? Ktoś pomyślał, że taki sześcian musi mieć krawędzie równoległe do osi współrzędnych. I wtedy to prawda. Ale przecież można wziąć obrócony sześcian, o, zaraz Ci taki jeden narysuję. Proszę! Ma wierzchołki w punktach kratowych? Ma!
- Loluś, ale on akurat ma krawędź całkowitej długości...
- No nie żartuj... 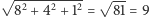 ... rzeczywiście! Patrz, jak mi się przyfarciło! Ale chyba widzisz, że można trochę poeksperymentować ze współrzędnymi i przykład wyjdzie. Poza tym moralnie to nie może być prawda.
... rzeczywiście! Patrz, jak mi się przyfarciło! Ale chyba widzisz, że można trochę poeksperymentować ze współrzędnymi i przykład wyjdzie. Poza tym moralnie to nie może być prawda.
- Moralnie?
- Tak, bo na płaszczyźnie to nieprawda. Zdanie jeżeli kwadrat na płaszczyźnie ma wszystkie wierzchołki w punktach kratowych, to jego bok ma całkowitą długość jest fałszywe: bez problemu można narysować taki kwadrat o boku 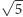 albo nawet
albo nawet 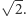
- I jak to się ma do sześcianu?
- Tak od razu to nijak. Ale mówiłem, że to moralny argument: skoro na płaszczyźnie analogiczne twierdzenie nie zachodzi, to co dopiero w przestrzeni, gdzie można dużo dowolniej manipulować współrzędnymi!
- Mnie te moralne argumenty jakoś nie przekonują. Na prostej wszystko gra.
- Na prostej?
- No tak, zobacz: jeżeli odcinek na prostej ma oba końce w punktach kratowych, to jego długość jest liczbą całkowitą.
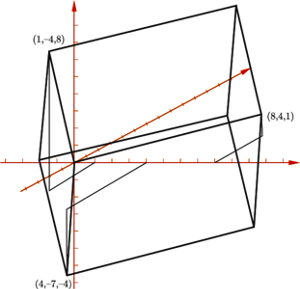
- Teraz to ale Amerykę odkryłeś... Dobra, już dobra, skonstruuję Ci precyzyjny kontrprzykład.
Jaką długość krawędzi byś chciał?
- To ja poproszę 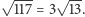
- Ambitnie! Ale dobra, niech będzie. Więc tak: jeden wierzchołek będzie w punkcie 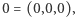 następny w jakimś punkcie odległym o
następny w jakimś punkcie odległym o 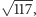 na przykład...
na przykład... 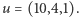 Teraz zgadniemy sobie jakiś wektor
Teraz zgadniemy sobie jakiś wektor  prostopadły do
prostopadły do  i tej samej długości. Powiedzmy, no... czekaj... mam:
i tej samej długości. Powiedzmy, no... czekaj... mam: 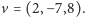
- Na pewno są prostopadłe?
- Nie wierzysz mi? Odległość między ich końcami wynosi
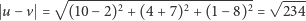
i mamy
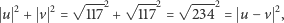
więc kąt między 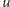 i
i  jest prosty z twierdzenia Pitagorasa.
jest prosty z twierdzenia Pitagorasa.
- Chyba z twierdzenia odwrotnego do...
- Cicho siedź! Pedant się znalazł. Poza tym łatwo sprawdzić, że Twoje pytanie sprowadza się do obliczenia iloczynu skalarnego
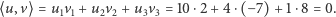
Skoro wyszło 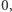 to kąt jest prosty. Uczyłem się o tym na matematyce. Więc podsumujmy: punkty
to kąt jest prosty. Uczyłem się o tym na matematyce. Więc podsumujmy: punkty 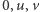 i
i 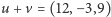 wyznaczają kwadrat o boku
wyznaczają kwadrat o boku 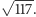 Zgadza się?
Zgadza się?
- Na razie dobrze.
- To będzie podstawa naszego sześcianu. Teraz wystarczy znaleźć trzeci wektor 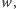 prostopadły do obu
prostopadły do obu  i
i 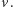 Ugh... to chyba potrwa. Przynieś coś do picia.
Ugh... to chyba potrwa. Przynieś coś do picia.
- Czekaj, o tym to ja się uczyłem na fizyce. To się nazywa iloczyn wektorowy 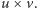 Podstawia się dwa wektory i wychodzi wektor prostopadły do nich obu, czyli w Twojej notacji
Podstawia się dwa wektory i wychodzi wektor prostopadły do nich obu, czyli w Twojej notacji 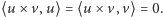 Chcesz wzór?
Chcesz wzór?
- Dawaj!
- Mam go tu w zeszycie. Uwaga: 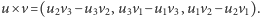
- Trochę długi, ale to nic, podstawiamy: 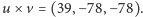 To już, bierzemy wektory
To już, bierzemy wektory 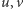 i
i 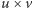 i rozpinamy na nich sześcian! A nie mówiłem!
i rozpinamy na nich sześcian! A nie mówiłem!
- Za bardzo się rozpędziłeś. Ten Twój "sześcian" to tylko prostopadłościan. Trzeci wektor ma długość 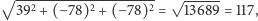 a nie
a nie 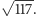 Zapomniałem Ci powiedzieć: długość wektora
Zapomniałem Ci powiedzieć: długość wektora 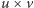 jest równa polu równoległoboku rozpiętego przez
jest równa polu równoległoboku rozpiętego przez  i
i 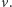
- Czyli w naszym przypadku polu kwadratu: 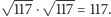 To by się nawet zgadzało. Ehhh... Ale zaraz, nie wystarczy przeskalować ten wektor? Kierunek jest przecież dobry, tylko długość się nie zgadza!
To by się nawet zgadzało. Ehhh... Ale zaraz, nie wystarczy przeskalować ten wektor? Kierunek jest przecież dobry, tylko długość się nie zgadza!
- Bingo! Mamy wektor o długości 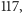 a chcieliśmy
a chcieliśmy 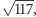 czyli trzeba każdą współrzędną podzielić przez
czyli trzeba każdą współrzędną podzielić przez 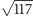 ! No nie... to niedobrze. Wychodzi
! No nie... to niedobrze. Wychodzi 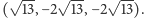 To nie jest punkt o współrzędnych całkowitych.
To nie jest punkt o współrzędnych całkowitych.
- Widzę właśnie. No trudno. Pierwsze koty za płoty. Weźmiemy jakieś inne  i
i 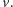 A jak znowu się nie uda, to zmienimy ten
A jak znowu się nie uda, to zmienimy ten 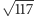 na
na 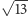 albo
albo 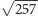 i na pewno w końcu znajdziemy dobry przykład. A tak w ogóle, to czemu ja mam się męczyć? Bolek, Ty miałeś informatykę, weź to zaprogramuj i niech komputer szuka. W jakim języku wy się tam uczycie?
i na pewno w końcu znajdziemy dobry przykład. A tak w ogóle, to czemu ja mam się męczyć? Bolek, Ty miałeś informatykę, weź to zaprogramuj i niech komputer szuka. W jakim języku wy się tam uczycie?
- W COBOLu. Ale wiesz co, to chyba nie jest najlepszy pomysł...
- Bo co? Paru prostych pętli w COBOLu nie umiesz napisać? Nie bądź cienias!
- Nie no, umiem. Ale to chyba nic nie da, bo ja już widzę jak to się skończy.
- To weź mnie oświeć...
- Powiedzmy, że będziemy chcieli zrobić taką konstrukcję, biorąc za krawędź 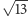 albo
albo 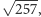 albo w ogóle
albo w ogóle 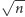 dla jakiegoś naturalnego
dla jakiegoś naturalnego 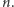 Wybierzemy dwa prostopadłe wektory
Wybierzemy dwa prostopadłe wektory  i
i  długości
długości 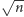 i całkowitych współrzędnych tak jak Ty...
i całkowitych współrzędnych tak jak Ty...
- Wybierzemy albo i nie. Skąd wiesz, że zawsze się da?
- Nieważne, jak się nie da, to i tak nici z konstrukcji, więc powiedzmy, że się udało. Teraz obliczasz wektor 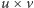 i tak jak poprzednio, on ma współrzędne całkowite i długość
i tak jak poprzednio, on ma współrzędne całkowite i długość 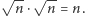 Czyli jest za długi, bo miało być
Czyli jest za długi, bo miało być 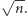 Więc musimy go skrócić
Więc musimy go skrócić 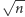 razy, bo tylko tam może być trzeci wierzchołek sześcianu...
razy, bo tylko tam może być trzeci wierzchołek sześcianu...
- Nie tylko tam, jeszcze po przeciwnej stronie!
- Teraz to Ty jesteś pedantem. Znak nic nie zmieni, bo tak czy inaczej wektor 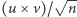 nie ma współrzędnych całkowitych, tylko niewymierne, bo wszędzie się kręci ten nieszczęsny
nie ma współrzędnych całkowitych, tylko niewymierne, bo wszędzie się kręci ten nieszczęsny 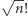
- Chyba że...
- Że co?
- ...że 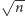 jest całkowity. Na przykład
jest całkowity. Na przykład 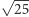 albo
albo 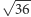 !
!

- Czyli już! No bo tak jakby pokazaliśmy, że nie da się skonstruować kontrprzykładu. A to chyba to samo, co udowodnić twierdzenie?
- Tak myślę. Weź, zapiszmy to jakoś zgrabnie i możemy opublikować na tym forum.
- Nie ma sensu, tam już jest jedno rozwiązanie.
- Tam już jest... Co? Bolek, Ty mnie zapędzasz w kozi róg, a tam już czeka gotowe rozwiązanie?! Czekaj, jak ja cię dorwę...
- Lolek, czekaj, ała! To nie tak! Bo ja tego rozwiązania z forum tak do końca nie rozumiem! Ono jest jakieś magiczne. Twoje jest dużo lepsze.
- Dobra, przeczytajmy razem, co oni tam piszą. Objętość sześcianu o krawędzi 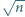 wynosi
wynosi 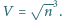 Na razie chyba wszystko jasne?
Na razie chyba wszystko jasne?
- Tak, tak. Ale patrz dalej: Ponieważ wszystkie wierzchołki mają współrzędne całkowite, więc objętość 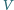 jest liczbą całkowitą. Tego do końca nie rozumiem. Dalej już jest łatwo: Z równości
jest liczbą całkowitą. Tego do końca nie rozumiem. Dalej już jest łatwo: Z równości 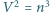 wynika, że
wynika, że 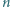 jest kwadratem liczby całkowitej, czyli krawędź
jest kwadratem liczby całkowitej, czyli krawędź 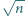 jest całkowita.
jest całkowita.
- Faktycznie magia. To jak to jest z tą objętością? Jest jakiś oczywisty powód, że sześcian o wierzchołkach w punktach kratowych musi mieć całkowitą objętość?
- Trochę o tym myślałem i wydaje mi się, że to może być prawda nawet dla dowolnego równoległościanu. Bo, na przykład, na płaszczyźnie wszystko działa: wzór na pole równoległoboku rozpiętego przez wektory 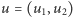 i
i 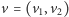 to
to 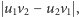 więc dla współrzędnych całkowitych wynik jest liczbą całkowitą. W przestrzeni też powinien być podobny wzór na objętość. Prawda?
więc dla współrzędnych całkowitych wynik jest liczbą całkowitą. W przestrzeni też powinien być podobny wzór na objętość. Prawda?
- Wiesz co, Bolek?
- No co?
- Myślałem, że Ciebie nie ruszają takie moralne argumenty.