Najpiękniejsze zadanie geometryczne
Znam takie zadanie. Jego autorem jest Igor Fiodorowicz Szarygin. Jego treść jest nieskomplikowana: jak szeroki walec można włożyć pomiędzy trzy jednakowe, parami prostopadłe walce?
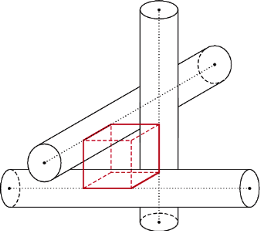
Rys. 1
Purysta zażądałby doprecyzowania. Ale człowiek rozsądny nie będzie miał wątpliwości, że chodzi o rezultat ekstremalny, a więc o najmniej korzystną dla wkładanego walca sytuację. A więc walce o osiach parami prostopadłych mają być styczne (bo wtedy miejsca na wkładany walec będzie najmniej).
W rozwiązaniu tego zadania kluczowe jest dostrzeżenie w danych trzech walcach sześcianu. Odkrywa się jego istnienie w następujący sposób.
Osie dwóch walców to proste skośne. Dla prostych skośnych zaś istnieje łączący je odcinek prostopadły do obu z nich - to najkrótsze ich połączenie.
Tu dygresja dla niedowiarków. Gdy proste 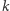 i
i 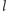 są skośne, przez dowolny punkt prostej
są skośne, przez dowolny punkt prostej 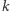 prowadzimy prostą
prowadzimy prostą 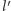 równoległą do
równoległą do 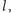 a przez dowolny punkt prostej
a przez dowolny punkt prostej 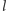 prostą
prostą 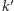 równoległą do
równoległą do 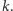 Płaszczyzny
Płaszczyzny 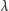 zawierająca proste
zawierająca proste 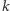 i
i 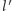 oraz
oraz 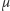 zawierająca proste
zawierająca proste 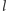 i
i 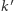 są równoległe. Płaszczyzna
są równoległe. Płaszczyzna 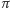 zawierająca prostą
zawierająca prostą 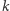 i prostopadła do
i prostopadła do 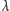 i płaszczyzna
i płaszczyzna 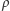 zawierająca prostą
zawierająca prostą 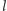 i prostopadła do płaszczyzny
i prostopadła do płaszczyzny 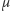 przecinają się wzdłuż odcinka łączącego
przecinają się wzdłuż odcinka łączącego 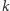 z
z 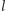 i prostopadłego do nich obu. Nieprawdaż?
i prostopadłego do nich obu. Nieprawdaż?
Odcinki prostopadłe łączące osie walców dla stycznych walców o promieniu 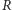 mają więc długość
mają więc długość 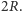 Co więcej, ich końce na każdej z osi walców są odległe też o
Co więcej, ich końce na każdej z osi walców są odległe też o 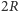 - połączmy je. Powstaje w ten sposób łamana złożona z sześciu odcinków (na rysunku 1 ciągłe odcinki kolorowe). Uzupełnienie jej do sześcianu nie sprawi nikomu kłopotu.
- połączmy je. Powstaje w ten sposób łamana złożona z sześciu odcinków (na rysunku 1 ciągłe odcinki kolorowe). Uzupełnienie jej do sześcianu nie sprawi nikomu kłopotu.
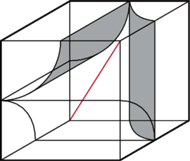
Rys. 2
Sześcian ten zawiera w sobie wszystko, co może mieć związek z wkładanym między walce poszukiwanym walcem. Jeśli narysujemy (wyobrazimy sobie), co się dzieje we wnętrzu sześcianu, zobaczymy trzy "ćwiartki" walców (Rys. 2). Tu następne kluczowe (ile jeszcze tych kluczy?) spostrzeżenie - te ćwiartki mają oś obrotową: prosta łącząca dorysowane na rysunku 1 wierzchołki sześcianu ma tę własność, że obracając wokół niej owe ćwiartki (można to robić razem z sześcianem), otrzymujemy tę samą sytuację. Zauważmy, że owa oś jest też osią obrotową dla danych na początku walców. Jest ona, oczywiście, jednakowo odległa od każdej z ćwiartek, a każda inna prosta, biegnąca między ćwiartkami, jest w mniejszej odległości od co najmniej jednej z nich.

Rys. 3
Tak więc znaleźliśmy oś poszukiwanego walca, a jego promień to jej odległość od którejkolwiek z ćwiartek.
No to kolejne kluczowe spostrzeżenie: przy zrzutowaniu w kierunki równoległym do powierzchni ćwiartki odległość jej od osi nie powiększa się. I tak nasze stereometryczne zadanie zredukowało się do zadania płaskiego (Rys. 3): jaka jest odległość przekątnej kwadratu u boku 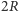 od okręgu mającego środek w wierzchołku kwadratu i promień
od okręgu mającego środek w wierzchołku kwadratu i promień 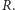
To, że wynikiem jest 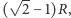 nie budzi wątpliwości.
nie budzi wątpliwości.
Zadanie to podziwiam dlatego, że prezentuje rzecz dla mnie w matematyce najpiękniejszą - redukcję zawiłości do sedna sprawy.