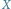Rzut butem, czyli twierdzenie Chaslesa
Niedawno podczas rozmowy z kolegami - młodymi matematykami i fizykami - zorientowałem się, że dla nich informacja o tym, jak wyglądają wszystkie możliwe ruchy obiektu materialnego w trójwymiarowej przestrzeni, jest zaskakująca...
Chodzi o następujący obrazowy opis.
Zdjąłem z nogi but i cisnąłem nim byle jak, po czym on upadł byle gdzie i jakoś tam leży. Istnieje ruch po linii śrubowej, za pomocą którego można kulturalnie przenieść ten but z obecnego położenia na moją nogę.
Wyrażając się żargonowo (czyli fachowo), można powyższą anegdotę wyrazić zdaniem
każda niezmieniająca orientacji izometria przestrzeni trójwymiarowej jest ruchem śrubowym, czyli złożeniem obrotu z przesunięciem równoległym do jego osi.
Jest to fragment twierdzenia Michela Chaslesa (czyt. Szala), w którym sklasyfikował on wszelkie izometrie (czyli przekształcenia niezmieniające odległości) na płaszczyźnie i w przestrzeni.
Słowo "orientacja" użyte wyżej tłumaczy, dlaczego w anegdotce rzucałem butem - żaden rzut nie zmieni buta prawego na lewy ani lewego na prawy.
Zamiast ubolewać nad nieświadomością młodego pokolenia, przyjrzyjmy się temu twierdzeniu.
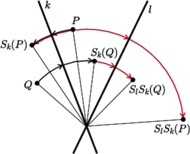
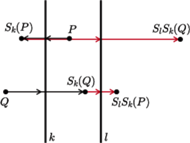
Rys. 1 Gdy 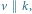 kolejność wykonywania przesunięcia i symetrii jest dowolna
kolejność wykonywania przesunięcia i symetrii jest dowolna
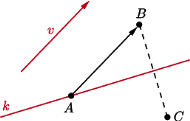
Rys. 2 Gdy 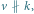 obrazem punktu
obrazem punktu 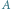 w przesunięciu i symetrii będzie punkt
w przesunięciu i symetrii będzie punkt 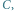 a w symetrii i przesunięciu punkt
a w symetrii i przesunięciu punkt 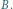
Oto pełne brzmienie
Twierdzenie (Chaslesa dla płaszczyzny). Każda izometria płaszczyzny jest przesunięciem, obrotem lub symetrią z poślizgiem (czyli złożeniem symetrii osiowej z przesunięciem równoległym do jej osi). Orientację zachowują pierwsze dwa z tych przekształceń.
Dla przestrzeni wygląda ono tak.
Twierdzenie (Chaslesa dla przestrzeni). Każda izometria przestrzeni to ruch śrubowy, symetria z poślizgiem (czyli złożenie symetrii płaszczyznowej z przesunięciem o wektor równoległy do tej płaszczyzny) lub symetria obrotowa (czyli złożenie symetrii płaszczyznowej z obrotem względem prostej prostopadłej do tej płaszczyzny).
W obu tych twierdzeniach, obok przesunięć i obrotów, występują raczej egzotyczne dla ogółu nazwy - czemu Chasles zwrócił uwagę akurat na takie przekształcenia? Odpowiedź jest zaskakująco prosta: w każdym z nich kolejność wykonywania ich składowych przekształceń nie ma wpływu na wynik, czyli ich składanie jest przemienne. Obojętne jest, czy mając w przestrzeni obrót względem prostej i przesunięcie o wektor równoległy do tej prostej, najpierw wykonamy obrót, a potem przesunięcie, czy też najpierw przesunięcie, a potem obrót. Podobnie jest w pozostałych przypadkach. Jeszcze ciekawsze jest to, że składanie przesunięć, obrotów i symetrii przemienne jest tylko w wymienionych w twierdzeniach Chaslesa przypadkach. Łatwo objaśnić to na obrazkach - w przypadku symetrii z poślizgiem na płaszczyźnie demonstrują to rysunki 1 i 2.

Rys. 3 Jeśli  jest punktem stałym, obraz
jest punktem stałym, obraz 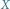 pozostaje na
pozostaje na 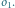 Gdy również
Gdy również 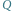 jest punktem stałym, obraz
jest punktem stałym, obraz 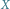 pozostaje na
pozostaje na  a zatem nie rusza się
a zatem nie rusza się
Rys. 4 Jeśli  są punktami stałymi, stałe są wszystkie punkty prostych
są punktami stałymi, stałe są wszystkie punkty prostych  Zatem prosta przechodząca przez
Zatem prosta przechodząca przez 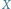 i przecinająca dwie z tych prostych ma dwa punkty stałe, stąd stałe są wszystkie jej punkty, a więc i
i przecinająca dwie z tych prostych ma dwa punkty stałe, stąd stałe są wszystkie jej punkty, a więc i 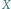
Droga do dowodu twierdzenia Chaslesa wiedzie przez wykazanie, że każdą izometrię można uzyskać przez złożenie symetrii osiowych w przypadku płaszczyzny czy płaszczyznowych w przypadku przestrzeni.
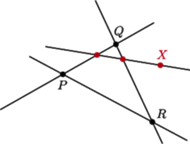
W tym celu przyjrzyjmy się punktom stałym izometrii. Gdy izometria ma punkt stały 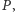 to zachowuje ona okręgi o środku w
to zachowuje ona okręgi o środku w 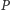 w przypadku płaszczyzny i sfery o środku w
w przypadku płaszczyzny i sfery o środku w 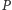 w przypadku przestrzeni. Gdy stały jest jeszcze inny punkt
w przypadku przestrzeni. Gdy stały jest jeszcze inny punkt 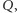 to w obu przypadkach wszystkie punkty prostej
to w obu przypadkach wszystkie punkty prostej 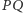 są stałe (Rys. 3). Gdy na dodatek stały jest jeszcze pewien punkt
są stałe (Rys. 3). Gdy na dodatek stały jest jeszcze pewien punkt 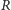 nieleżący na tej prostej, to stałe są wszystkie punkty płaszczyzny
nieleżący na tej prostej, to stałe są wszystkie punkty płaszczyzny 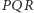 (Rys. 4).
(Rys. 4).
Gdy mamy do czynienia z przestrzenią, są jeszcze punkty poza tą płaszczyzną - Czytelnik Sprawny w mgnieniu oka przystosuje rozumowanie z rysunku 4 do wykazania, że gdy istnieje wśród nich punkt stały, to stałe są wszystkie punkty przestrzeni. Zatem
Twierdzenie. Jeśli izometria ma trzy niewspółliniowe punkty stale na płaszczyźnie (cztery niewspółpłaszczyznowe punkty stałe w przestrzeni), to jest identycznością.
Twierdzenie to nazywa się małym twierdzeniem o sztywności. Ale jest i duże.
Twierdzenie. Jeśli dwie izometrie pokrywają się na trzech niewspółliniowych punktach płaszczyzny (czterech niewspółpłaszczyznowych punktach przestrzeni), to są jednakowe.
Istotnie, jeśli te izometrie to 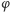 i
i 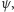 to izometria
to izometria 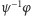 jest w myśl małego twierdzenia o sztywności identycznością, mamy więc
jest w myśl małego twierdzenia o sztywności identycznością, mamy więc

Kolejny krok to
Twierdzenie (o rozkładzie). Każda izometria może być przedstawiona jako złożenie co najwyżej trzech symetrii osiowych w przypadku płaszczyzny (czterech symetrii płaszczyznowych w przypadku przestrzeni).
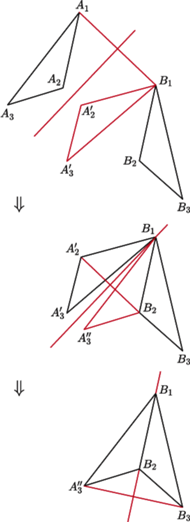
Rys. 5
Oto recepta na ich znalezienie. Zajmijmy się płaszczyzną. W myśl twierdzenia o sztywności wystarczy pokazać złożenie trzech symetrii, które nałoży dane dwa trójkąty przystające, nazwijmy je  i
i  Przepis jest następujący.
Przepis jest następujący.
Jeśli
wykonaj symetrię trójkąta
względem symetralnej odcinka
otrzymasz trójkąt
Jeśli teraz
wykonaj symetrię trójkąta
względem symetralnej odcinka
otrzymasz trójkąt
Jeśli jeszcze
wykonaj symetrię trójkąta
względem symetralnej odcinka
(Czytelnik Zinformatyzowany oczywiście w mgnieniu oka zamieni ten przepis na króciutki pseudokod.)
Działanie tego przepisu w przypadku, gdy aż trzy razy trzeba zastosować symetrię, przedstawia rysunek 5. To, nad czym trzeba chwilę się zastanowić, to fakt, że kolejna symetria nie "rozkleja" już nałożonych punktów - gwarantuje to założone przystawanie trójkątów.
Każdy Czytelnik, który doczytał do tego miejsca, bez trudu poradzi sobie z podaniem analogicznego przepisu dla przestrzeni (przypominam, że symetralna odcinka w przestrzeni jest płaszczyzną).
Warto zwrócić uwagę na bezpośrednie wnioski z twierdzeń o sztywności, jakie w szczególnych przypadkach wzmacniają twierdzenie o rozkładzie. Jeśli np. izometria płaszczyzny ma punkt stały, to zawsze da się rozłożyć na co najwyżej dwie symetrie, a gdy ma dwa punkty stałe, to jest symetrią lub identycznością. Podobnie jest w przypadku izometrii przestrzeni - gdy wiemy, że są punkty stałe, liczba niezbędnych symetrii do jej uzyskania zmniejsza się.
Rys. 6
Rys. 7
Przypomnijmy teraz sobie (bo przecież wszyscy to wiedzą lub wiedzieli), że złożenie dwóch symetrii względem przecinających się prostych na płaszczyźnie (płaszczyzn w przestrzeni) to obrót o kąt dwukrotnie większy niż między nimi (Rys. 6). Podobnie, złożenie dwóch symetrii względem prostych równoległych na płaszczyźnie (płaszczyzn równoległych w przestrzeni) jest przesunięciem o wektor dwukrotnie większy niż między nimi (Rys. 7).
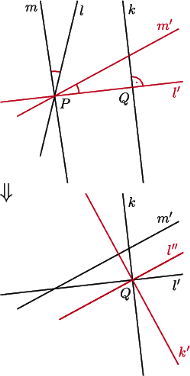
Rys. 8
Pozwala to na stwierdzenie, że złożenie symetrii względem trzech prostych na płaszczyźnie jest zawsze symetrią z poślizgiem. Rozpatrzmy przypadek szczególny: składamy symetrie względem prostych 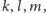 przy czym
przy czym 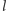 i
i  mają punkt wspólny
mają punkt wspólny 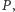 przez który prosta
przez który prosta 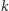 nie przechodzi. Wtedy zastępujemy proste
nie przechodzi. Wtedy zastępujemy proste 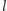 i
i 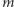 tworzącymi ten sam kąt prostymi
tworzącymi ten sam kąt prostymi 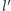 i
i 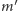 przechodzącymi przez
przechodzącymi przez 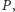 przy czym
przy czym 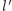 jest prostopadła do
jest prostopadła do 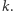 Jeśli chodzi o przekształcenie, to nic się nie zmieniło, bo
Jeśli chodzi o przekształcenie, to nic się nie zmieniło, bo  jest tym samym obrotem co
jest tym samym obrotem co 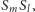 a więc
a więc

Oznaczmy punkt przecięcia prostopadłych prostych 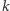 i
i 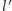 przez
przez 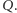 Teraz zastąpimy te proste przez inne przechodzące przez
Teraz zastąpimy te proste przez inne przechodzące przez 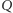 proste prostopadłe
proste prostopadłe 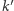 i
i 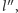 takie, że
takie, że 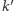 jest prostopadła do
jest prostopadła do 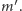 I znów mamy (Rys. 8)
I znów mamy (Rys. 8)

czyli nasze przekształcenie okazało się złożeniem symetrii względem 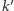 i przesunięciem o podwojony wektor łączący prostopadle
i przesunięciem o podwojony wektor łączący prostopadle 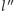 i
i 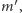 czyli symetrią z poślizgiem.
czyli symetrią z poślizgiem.
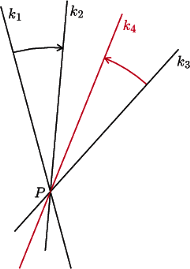
Rys. 9
Czytelnik Nieufny może teraz powtórzyć podobne operacje w innych możliwych przypadkach położenia trzech prostych na płaszczyźnie. No i oczywiście natknie się na sytuacje, w których jest to niemożliwe - mianowicie wtedy, gdy trzy osie symetrii mają wspólny kierunek albo też wspólny punkt. Na szczęście sytuację tę reguluje
Twierdzenie (o redukcji). Na płaszczyźnie złożenie symetrii względem trzech prostych mających wspólny punkt (lub kierunek) można zastąpić jedną symetrią względem prostej również przechodzącą przez ten punkt (mającą ten kierunek). W przestrzeni złożenie symetrii względem trzech płaszczyzn mających wspólną prostą (lub parami równoległych) można zastąpić jedną symetrią względem płaszczyzny również przechodzącej przez tę prostą (równoległą do nich).
Weźmy bowiem pod uwagę trzy proste 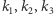 na płaszczyźnie (płaszczyzny
na płaszczyźnie (płaszczyzny 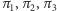 w przestrzeni) mające wspólny punkt
w przestrzeni) mające wspólny punkt 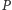 (wspólną prostą
(wspólną prostą 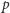 ). Jeśli kąt od
). Jeśli kąt od 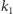 do
do 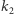 jest równy
jest równy 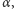 to zastępującą je prostą (płaszczyzną) jest taka prosta
to zastępującą je prostą (płaszczyzną) jest taka prosta 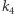 (płaszczyzna
(płaszczyzna 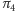 ) przechodząca przez
) przechodząca przez 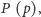 że kąt od
że kąt od 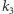 do
do 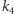 (od
(od 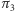 do
do 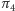 ) jest równy
) jest równy 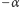 (Rys. 9). Wówczas
(Rys. 9). Wówczas 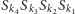 jest obrotem o kąt
jest obrotem o kąt 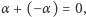 czyli jest identycznością. A więc mamy
czyli jest identycznością. A więc mamy

zatem

czyli

i tak samo będzie dla płaszczyzn.
Zupełnie analogicznie postępujemy w przypadku, gdy proste (płaszczyzny) są równoległe: gdy wektor łączący prostopadle 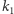 i
i 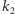 (czy
(czy  i
i 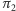 ) to
) to 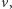 jako
jako 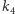 bierzemy taką prostą (płaszczyznę
bierzemy taką prostą (płaszczyznę 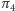 ) równoległą do danych, którą z
) równoległą do danych, którą z 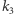 (z
(z 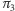 ) łączy wektor
) łączy wektor 
A więc w przypadku płaszczyzny ze złożenia trzech symetrii otrzymujemy zawsze symetrię z poślizgiem - być może zerowym.
Gdy chcemy stwierdzić jednak, jak wyglądają izometrie powstałe ze złożenia symetrii względem trzech płaszczyzn niespełniających założeń twierdzenia o redukcji, sytuacja nie jest już tak bezproblemowa.
Jak wiadomo (czy na pewno wiadomo?), dowolne trzy płaszczyzny mają wspólny punkt lub wspólną płaszczyznę prostopadłą.
Ten drugi przypadek jest powtórzeniem sytuacji z płaszczyzny (tak, jak byśmy patrzyli prostopadle do tej wspólnej prostopadłej). Tak więc symetrie z poślizgiem w przestrzeni mamy załatwione.
Pozostaje zbadać, co się dzieje, gdy składamy trzy symetrie względem płaszczyzn mających punkt wspólny 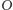 - nazwijmy wynik tego złożenia
- nazwijmy wynik tego złożenia 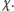 Dogodnym chwytem jest tu złożenie
Dogodnym chwytem jest tu złożenie 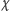 z symetrią względem
z symetrią względem 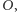 oznaczmy ją
oznaczmy ją 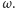 Symetria względem punktu w przestrzeni to złożenie trzech symetrii płaszczyznowych względem płaszczyzn prostopadłych (w układzie współrzędnych byłoby to
Symetria względem punktu w przestrzeni to złożenie trzech symetrii płaszczyznowych względem płaszczyzn prostopadłych (w układzie współrzędnych byłoby to 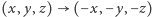 ). Otrzymujemy zatem złożenie sześciu symetrii płaszczyznowych, co wobec uwag po twierdzeniu o rozkładzie (jest punkt stały!) oznacza, iż jest to obrót względem jakiejś prostej przez
). Otrzymujemy zatem złożenie sześciu symetrii płaszczyznowych, co wobec uwag po twierdzeniu o rozkładzie (jest punkt stały!) oznacza, iż jest to obrót względem jakiejś prostej przez 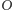 - oznaczmy ją
- oznaczmy ją 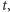 a sam obrót przez
a sam obrót przez 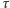 (istotnie, złożenie sześciu symetrii da się przedstawić jako złożenie czterech, a punkt stały zmniejsza to do trzech; z kolei fakt, że sześć symetrii płaszczyznowych nie zmienia orientacji, zmniejsza trzy do dwóch). Mamy więc
(istotnie, złożenie sześciu symetrii da się przedstawić jako złożenie czterech, a punkt stały zmniejsza to do trzech; z kolei fakt, że sześć symetrii płaszczyznowych nie zmienia orientacji, zmniejsza trzy do dwóch). Mamy więc 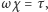 a więc
a więc 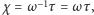 gdyż symetria względem punktu jest (jak wszystkie symetrie) inwolucją, czyli jest odwrotna sama do siebie.
gdyż symetria względem punktu jest (jak wszystkie symetrie) inwolucją, czyli jest odwrotna sama do siebie.
Trzy symetrie składające się na 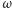 możemy dobrać tak, by dwie z nich były symetriami względem dowolnych płaszczyzn prostopadłych przechodzących przez
możemy dobrać tak, by dwie z nich były symetriami względem dowolnych płaszczyzn prostopadłych przechodzących przez 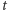 - trzecia wobec tego będzie do
- trzecia wobec tego będzie do 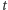 prostopadła. Korzystając z tych oznaczeń, mamy dwa obroty względem
prostopadła. Korzystając z tych oznaczeń, mamy dwa obroty względem 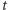 : jeden z nich to
: jeden z nich to 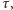 a drugi to symetria o osi
a drugi to symetria o osi 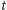 - czyli w sumie jeden obrót o kąt sumaryczny - oraz symetrię względem płaszczyzny prostopadłej do
- czyli w sumie jeden obrót o kąt sumaryczny - oraz symetrię względem płaszczyzny prostopadłej do 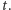 Zatem
Zatem 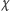 rzeczywiście jest symetrią obrotową.
rzeczywiście jest symetrią obrotową.
I w ten sposób pozostało nam już tylko rozpatrzenie sytuacji, gdy izometria przestrzeni jest złożeniem czterech symetrii płaszczyznowych i nie ma punktów stałych.
W tym celu weźmy pod uwagę jakąś izometrię 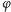 niezmieniającą orientacji i niech ona przeprowadza pewien punkt
niezmieniającą orientacji i niech ona przeprowadza pewien punkt 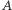 na
na 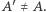 Oznaczmy przez
Oznaczmy przez 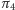 symetralną
symetralną 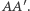 Przekształcenie
Przekształcenie 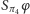 zmienia orientację i ma punkt stały (mianowicie
zmienia orientację i ma punkt stały (mianowicie 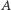 ) - jest zatem symetrią obrotową. Mamy więc
) - jest zatem symetrią obrotową. Mamy więc 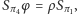 gdzie
gdzie 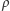 jest obrotem (oznaczmy jego oś przez
jest obrotem (oznaczmy jego oś przez 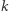 ), przy czym
), przy czym 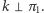 Przedstawmy
Przedstawmy 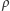 jako złożenie symetrii względem zawierających
jako złożenie symetrii względem zawierających 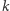 płaszczyzn
płaszczyzn 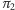 i
i 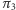 - jest tu (jak zawsze przy obrotach) duża dowolność - niech więc
- jest tu (jak zawsze przy obrotach) duża dowolność - niech więc 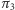 będzie prostopadła do
będzie prostopadła do 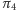 (oczywiście
(oczywiście 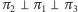 ).
).
Mamy więc 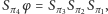 czyli
czyli 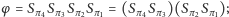 są to - wobec
są to - wobec  i
i  - dwie symetrie osiowe. Oznaczmy ich osie przez
- dwie symetrie osiowe. Oznaczmy ich osie przez 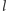 i
i 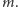 Zatem
Zatem 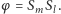 Proste
Proste 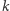 i
i 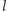 są skośne - gdyby były równoległe,
są skośne - gdyby były równoległe, 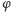 byłoby przesunięciem, a więc złożeniem dwóch symetrii płaszczyznowych, gdyby zaś się przecinały, istniałby punkt stały.
byłoby przesunięciem, a więc złożeniem dwóch symetrii płaszczyznowych, gdyby zaś się przecinały, istniałby punkt stały.

Rys. 10
Dowolne dwie proste skośne leżą w pewnych płaszczyznach równoległych - przedstawmy więc symetrie względem 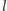 i
i 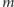 w następujący sposób (patrz Rys. 10):
w następujący sposób (patrz Rys. 10):

Zauważmy, że wtedy również płaszczyzny 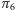 i
i 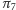 są prostopadłe, zatem
są prostopadłe, zatem

gdzie  to obrót o osi
to obrót o osi 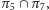 a
a 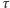 to przesunięcie wzdłuż tej osi.
to przesunięcie wzdłuż tej osi.
Twierdzenie Chaslesa dla przestrzeni zostało tym samym udowodnione.
Warto wiedzieć, że Chasles udowodnił również twierdzenia klasyfikujące podobieństwa na płaszczyźnie i w przestrzeni. Ale może o tym innym razem...
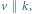 kolejność wykonywania przesunięcia i symetrii jest dowolna
kolejność wykonywania przesunięcia i symetrii jest dowolna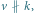 obrazem punktu
obrazem punktu 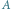 w przesunięciu i symetrii będzie punkt
w przesunięciu i symetrii będzie punkt 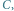 a w symetrii i przesunięciu punkt
a w symetrii i przesunięciu punkt 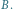
 jest punktem stałym, obraz
jest punktem stałym, obraz 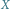 pozostaje na
pozostaje na 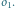 Gdy również
Gdy również 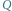 jest punktem stałym, obraz
jest punktem stałym, obraz 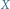 pozostaje na
pozostaje na 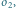 a zatem nie rusza się
a zatem nie rusza się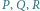 są punktami stałymi, stałe są wszystkie punkty prostych
są punktami stałymi, stałe są wszystkie punkty prostych 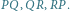 Zatem prosta przechodząca przez
Zatem prosta przechodząca przez  i przecinająca dwie z tych prostych ma dwa punkty stałe, stąd stałe są wszystkie jej punkty, a więc i
i przecinająca dwie z tych prostych ma dwa punkty stałe, stąd stałe są wszystkie jej punkty, a więc i