Wypełniane przestrzeni
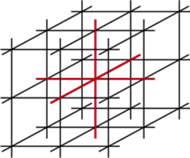
Problem wypełnienia przestrzeni bez luk jednakowymi wielościanami okazuje się wcale nie tak prosty, jak na pierwszy rzut oka można oczekiwać. Spośród pięciu wielościanów platońskich tylko jeden nadaje się do tego. Oczywiście, jest to sześcian...
O tym, że pozostałe nie mogą wypełnić przestrzeni, przekonać się łatwo: wystarczy zauważyć, że ich kąty dwuścienne nie składają się w żadnej liczbie na kąt pełny.
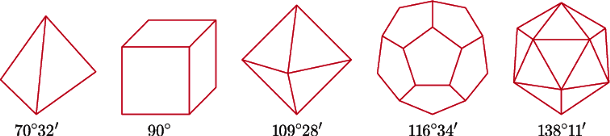
Wypełnienie przestrzeni sześcianami może być zrealizowane na wiele sposobów. Najbardziej oczywisty z nich to taki, gdy w każdym wierzchołku spotyka się 8 sześcianów. W tym wypełnieniu poszczególne wielościany stykają się całymi ścianami - wypełnienie o tej własności nazywa się normalne.

Minimalne wypełnienie sześcianami (widziane z kierunku jednej z krawędzi)
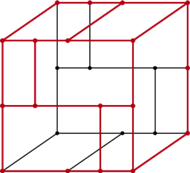
Sześcian jako czternastościan
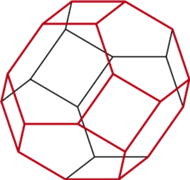
Czternastościan archimedesowy
Można jednak sześciany tak ułożone poprzesuwać w ten sposób, by w żadnym punkcie nie stykało się ich więcej niż 4. Liczby tej nie można już zmniejszyć. Henri Lebesgue zauważył w 1911 roku (a potem udowodnił), że w każdym wypełnieniu przestrzeni (już niekoniecznie jednakowymi) wielościanami będą punkty, gdzie stykać się ich będzie co najmniej 4. Przyjęto to nawet za jedną z wersji definicji wymiaru: jeśli jakąś przestrzeń można wypełnić tak, że są punkty, w których styka się 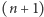 wypełniających obiektów i nie ma punktów, w których styka się ich więcej, to ma ona wymiar co najwyżej
wypełniających obiektów i nie ma punktów, w których styka się ich więcej, to ma ona wymiar co najwyżej 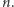 Zatem to nowe wypełnienie sześcianami realizuje minimum takiego
Zatem to nowe wypełnienie sześcianami realizuje minimum takiego  dla naszej przestrzeni, która jest trójwymiarowa. Wypełnienie realizujące minimum
dla naszej przestrzeni, która jest trójwymiarowa. Wypełnienie realizujące minimum  nazywa się, oczywiście, minimalne.
nazywa się, oczywiście, minimalne.
Mamy więc dla sześcianu wypełnienie normalne, mamy też wypełnienie minimalne, ale nie mamy wypełnienia, które miałoby równocześnie obie te własności. Powstaje pytanie, czy istnieje wielościan wypełniający przestrzeń i mający obie te własności.
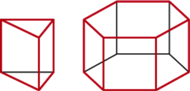
Wypełniające przestrzeń graniastosłupy archimedesowe (ten z prawej znany jest w budownictwie drogowym jako trylinka)
Piękną drogę do znalezienia pozytywnej odpowiedzi na to pytanie wskazał Hugo Steinhaus. Radzi on mianowicie, aby zaobserwować ślady, jakie na każdym sześcianie wypełnienia minimalnego zostawią krawędzie sąsiednich sześcianów. Widzimy, że są to prostokąty, z których 8 ma jednak po sześć śladów wierzchołków sąsiednich sześcianów. Można by je więc traktować jak sześciokąty. Przy takim podejściu nasz sześcian ma więc 8 ścian sześciokątnych i 6 czworokątnych, czyli jest czternastościanem. I nasuwa się pytanie, czy takiej bryły nie można zdeformować tak (nie zmieniając liczby obu rodzajów ścian), by wszystkie one stały się foremne.
Okazuje się, że jest to wykonalne, a otrzymany wielościan to czternastościan archimedesowy (wielościany archimedesowe mają wszystkie ściany foremne i jednakowe naroża). Można go inaczej otrzymać, obcinając ośmiościanowi foremnemu naroża do 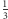 długości krawędzi. Okazuje się więc, że istnieje wielościan archimedesowy realizujący wypełnienie równocześnie normalne i minimalne. Można udowodnić, że jest on - wśród wielościanów mających ściany foremne - jedyny.
długości krawędzi. Okazuje się więc, że istnieje wielościan archimedesowy realizujący wypełnienie równocześnie normalne i minimalne. Można udowodnić, że jest on - wśród wielościanów mających ściany foremne - jedyny.
Jakie jeszcze wielościany archimedesowe mogą wypełnić przestrzeń? Tylko graniastosłupy o podstawach trójkątnych lub sześciokątnych (także czworokątnych, ale to są już wymienione sześciany). Wystarczy wypełnić płaszczyznę ich podstawami, by otrzymać warstwy w sposób oczywisty wypełniające przestrzeń.