Deltoid
Heron uogólniony?
Wzór Herona
 pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
pozwala wyznaczyć pole
trójkąta w zależności od długości jego boków (
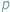 to połowa
obwodu). Czy da się go uogólnić, na przykład dla objętości czworościanu lub
pola czworokąta?
to połowa
obwodu). Czy da się go uogólnić, na przykład dla objętości czworościanu lub
pola czworokąta?
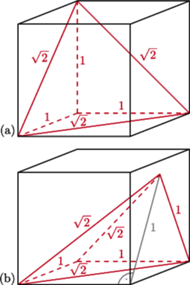
Rys. 1 Czarne sześciany i szara linia są pomocnicze. Na rysunku (b) górny wierzchołek czworościanu leży na prawej ścianie sześcianu, więc wysokość czworościanu jest mniejsza od 1.
Objętość czworościanu a pola jego ścian
W zadaniu 3 z poprzedniego deltoidu wykazaliśmy, że nie można obliczyć objętości czworościanu, znając jedynie pola jego ścian oraz promień kuli opisanej, tym bardziej więc same pola ścian nie wyznaczają objętości.
Warto zauważyć, że pola ścian i promień
 kuli wpisanej pozwalają
wyrazić objętość czworościanu. Istotnie, odcinki łączące środek kuli
z wierzchołkami czworościanu zadają podział na cztery ostrosłupy;
podstawą każdego z nich jest inna ściana czworościanu, a wysokość
każdego równa jest
kuli wpisanej pozwalają
wyrazić objętość czworościanu. Istotnie, odcinki łączące środek kuli
z wierzchołkami czworościanu zadają podział na cztery ostrosłupy;
podstawą każdego z nich jest inna ściana czworościanu, a wysokość
każdego równa jest
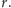 Stąd wzór na objętość czworościanu
Stąd wzór na objętość czworościanu
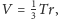 gdzie
gdzie
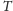 to pole jego powierzchni. Wzór ten jest jednak
raczej uogólnieniem wzoru na pole trójkąta
to pole jego powierzchni. Wzór ten jest jednak
raczej uogólnieniem wzoru na pole trójkąta
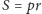 niż wzoru
Herona.
niż wzoru
Herona.
Objętość czworościanu a długości jego krawędzi
Same długości sześciu krawędzi, bez dodatkowej informacji o ich
konfiguracji, nie wyznaczają objętości czworościanu, co ilustruje para
kolorowych brył z rysunku 1 Mają one krawędzie o długościach
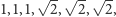 przystające podstawy, ale różne wysokości, więc
też różne objętości.
przystające podstawy, ale różne wysokości, więc
też różne objętości.
Długości wszystkich krawędzi wraz z ich konfiguracją definiują jednoznacznie czworościan, zatem też jego objętość. Niestety, w ogólnym przypadku wzór jest dość skomplikowany. Zajmijmy się więc szczególną klasą czworościanów równościennych – takich, których przeciwległe krawędzie są parami równe.

Rys. 2
Podobnie jak w poprzednim deltoidzie, opiszmy na takim czworościanie
równoległościan (Rys. 2). Jest on prostopadłościanem, gdyż każda z jego
ścian jest równoległobokiem o równych przekątnych, czyli prostokątem.
Przyjmijmy oznaczenia jak na rysunku 2 Z twierdzenia Pitagorasa otrzymujemy
wówczas
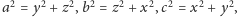 więc
więc
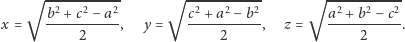 |
Objętość czworościanu równościennego to objętość prostopadłościanu pomniejszona o objętości czterech przystających naroży, czyli
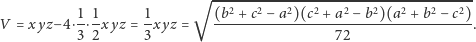 |
Pole czworokąta a długości jego boków
Wzór na pole czworokąta zależny wyłącznie od jego boków (nawet z uwzględnieniem ich kolejności) istnieć nie może – wystarczy spojrzeć na prostokąt i nieprostokątny równoległobok o takich samych bokach.
Na szczęście przy dodatkowych założeniach istnieją ładne uogólnienia wzoru Herona. Jeśli czworokąt jest wpisany w okrąg, zachodzi wzór Brahmagupty:
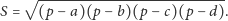 |
Jeśli zaś przez
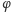 oznaczymy połowę sumy przeciwległych kątów
czworokąta (obojętne, których), a przez
oznaczymy połowę sumy przeciwległych kątów
czworokąta (obojętne, których), a przez
 i
i
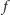 długości
przekątnych czworokąta, mamy dwa wzory Bretschneidera:
długości
przekątnych czworokąta, mamy dwa wzory Bretschneidera:
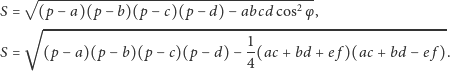
Dla czworokąta wpisanego w okrąg suma przeciwległych kątów równa jest
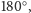 więc
więc
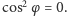 Z kolei twierdzenie Ptolemeusza orzeka, że
Z kolei twierdzenie Ptolemeusza orzeka, że
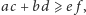 a równość zachodzi wtedy i tylko wtedy, gdy na
czworokącie można opisać okrąg. Zatem dla takiego czworokąta oba
powyższe wzory upraszczają się do wzoru Brahmagupty. Ponadto wynika stąd,
że czworokąt o ustalonych kolejnych bokach ma maksymalne pole właśnie
wtedy, gdy jest wpisany w okrąg.
a równość zachodzi wtedy i tylko wtedy, gdy na
czworokącie można opisać okrąg. Zatem dla takiego czworokąta oba
powyższe wzory upraszczają się do wzoru Brahmagupty. Ponadto wynika stąd,
że czworokąt o ustalonych kolejnych bokach ma maksymalne pole właśnie
wtedy, gdy jest wpisany w okrąg.
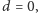 czyli dla czworokąta zdegenerowanego do trójkąta,
otrzymujemy wzór Herona.
czyli dla czworokąta zdegenerowanego do trójkąta,
otrzymujemy wzór Herona.