Lampy Catalana
Wielu projektantów często w swych koncepcjach odwołuje się do geometrycznych form, inspirując się harmonią, regularnościami i symetrią brył przestrzennych. Do takich twórców należy Tom Dixon, autor wielu innowacyjnych pomysłów. Podczas międzynarodowych targów sztuki użytkowej we Frankfurcie przedstawił projekt oświetlenia oparty na formach geometrycznych rzadko spotykanych w wystroju wnętrz. Zaprezentował lampy, których obudowy są powierzchniami brył Catalana...

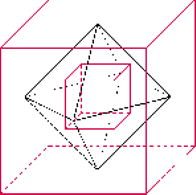
Rys. 1
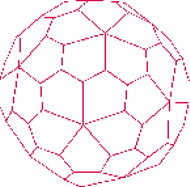
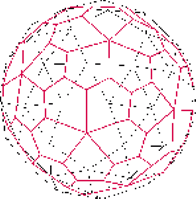
Rys. 2
Przyjrzyjmy się bliżej strukturze geometrycznej lampy z rysunku 1
Powierzchnia lampy składa się z przystających (ale nieforemnych!) pięciokątów i ma dwa typy naroży: takie, w których spotykają się trzy, i takie, w których styka się pięć ścian (Rys. 2). W narożach drugiego rodzaju, z których wychodzi po pięć krawędzi, pięciokąty stykają się kątami ostrymi. W pozostałych, z których wychodzą po trzy krawędzie, spotykają się kąty rozwarte.
Do opisania struktury żyrandola przyjmijmy następujące oznaczenia:
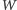 – liczba wierzchołków,
– liczba wierzchołków,
 – liczba wierzchołków, w których spotyka się pięć ścian,
– liczba wierzchołków, w których spotyka się pięć ścian,
 – liczba wierzchołków, w których spotykają się trzy ściany,
– liczba wierzchołków, w których spotykają się trzy ściany,
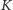 – liczba krawędzi,
– liczba krawędzi,
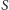 – liczba ścian.
– liczba ścian.

Rys. 3
Stwierdziliśmy już, że są tylko dwa rodzaje wierzchołków, co oznacza, że
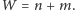 Ponadto, ponieważ każda ściana jest pięciokątem, więc
wszystkie ściany mają w sumie
Ponadto, ponieważ każda ściana jest pięciokątem, więc
wszystkie ściany mają w sumie
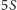 krawędzi. Musimy jednak pamiętać,
że każdą krawędź wielościanu liczymy podwójnie, ponieważ należy do
dwóch ścian (Rys. 3). Stąd
krawędzi. Musimy jednak pamiętać,
że każdą krawędź wielościanu liczymy podwójnie, ponieważ należy do
dwóch ścian (Rys. 3). Stąd
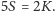

Rys. 4
Podobnie, z wierzchołków wychodzi w sumie
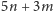 krawędzi, ale
znów policzyliśmy każdą krawędź dwukrotnie, raz dla każdego końca.
Wobec tego
krawędzi, ale
znów policzyliśmy każdą krawędź dwukrotnie, raz dla każdego końca.
Wobec tego
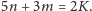 Możemy także zaobserwować, że każdy
wierzchołek z pięcioma wychodzącymi krawędziami jest środkiem
grupy pięciu pięciokątów (Rys. 4), i że takie grupy nie przecinają się
i pokrywają całą powierzchnię. Otrzymujemy więc
Możemy także zaobserwować, że każdy
wierzchołek z pięcioma wychodzącymi krawędziami jest środkiem
grupy pięciu pięciokątów (Rys. 4), i że takie grupy nie przecinają się
i pokrywają całą powierzchnię. Otrzymujemy więc
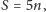 a stąd
a stąd
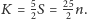
Przypomnijmy wzór Eulera na związek między liczbą wierzchołków, krawędzi
i ścian dowolnego wypukłego wielościanu:
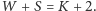 W naszym
przypadku, skoro
W naszym
przypadku, skoro
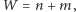
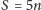 i
i
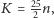 to
otrzymujemy
to
otrzymujemy
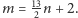 Z tej zależności, korzystając
z
Z tej zależności, korzystając
z
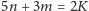 i jeszcze raz z
i jeszcze raz z
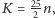 uzyskujemy:
uzyskujemy:
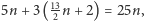 a zatem
a zatem
 Stąd już łatwo obliczyć
Stąd już łatwo obliczyć
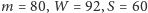 i
i
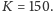 Podsumowując, nasza lampa
zbudowana jest z 60 ścian pięciokątnych i liczy 92 wierzchołki oraz 150
krawędzi.
Podsumowując, nasza lampa
zbudowana jest z 60 ścian pięciokątnych i liczy 92 wierzchołki oraz 150
krawędzi.
Ten wielościan to tak zwany sześćdziestościan pięciokątny. Jest reprezentantem grupy wielościanów opisanej prawie 150 lat temu przez belgijskiego matematyka Eugène’a Catalana. Badając grupę trzynastu brył archimedesowych (półforemnych – ściany foremne, niekoniecznie jednakowe, naroża jednakowe), Catalan skonstruował ich dualne odpowiedniki. Otrzymana w ten sposób rodzina brył ma wiele intrygujących własności. Wszystkie ściany takich brył są identyczne, choć nie są foremne. W każdą z nich można wpisać kulę styczną do wszystkich ścian. Są wśród nich egzemplarze, na podstawie których projektuje się piłki, ale również takie, którymi można całkowicie wypełnić przestrzeń, nie pozostawiając żadnych szczelin.

Rys. 8
Badana przez nas lampa jest dualna do bryły nazywanej dwudziesto-dwunastościanem przyciętym (Rys. 5). Wielościany dualne to pary brył, w których jedną otrzymuje się z drugiej (a drugą z pierwszej) przez połączenie krawędziami środków sąsiednich ścian wielościanu. Najprostszy przykład to sześcian i ośmiościan foremny (Rys. 6): łącząc środki ścian sześcianu dostajemy ośmiościan, a po połączeniu środków ścian ośmiościanu z powrotem mamy sześcian. W przypadku omawianej lampy łącząc odpowiednio środki ścian dwudziesto-dwunastościanu przyciętego, otrzymamy sześćdziestościan pięciokątny (Rys. 7).
Istnieją jeszcze inne eleganckie modele geometryczne, które „świecą przykładem”: w kolekcji Toma Dixona można znaleźć lampę w formie dwudziestoczterościanu deltoidowego (Rys. 8). Czytelnika Wnikliwego zachęcam do rozszyfrowania szczegółów jej konstrukcji.